
如圖所示的幾何體ABCDFE中,△ABC,△DFE都是等邊三角形,且所在平面平行,四邊形BCED是邊長為2的正方形,且所在平面垂直于平面ABC.
(Ⅰ)求幾何體ABCDFE的體積;
(Ⅱ)證明:平面ADE∥平面BCF;
科目:高中數(shù)學 來源: 題型:解答題
已知梯形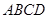 中
中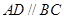 ,
,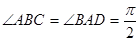 ,
,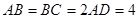 ,
,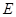 、
、 分別是
分別是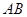 、
、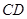 上的點,
上的點,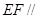
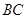 ,
,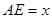 .沿
.沿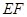 將梯形
將梯形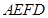 翻折,使平面
翻折,使平面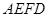 ⊥平面
⊥平面 (如圖).
(如圖).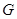 是
是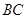 的中點.
的中點.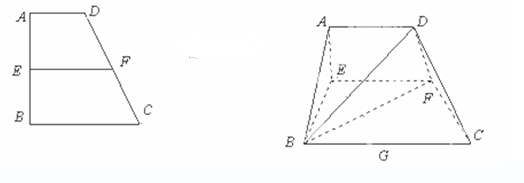
(1)當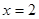 時,求證:
時,求證: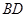 ⊥
⊥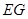 ;
;
(2)當 變化時,求三棱錐
變化時,求三棱錐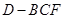 體積的最大值.
體積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,直三棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點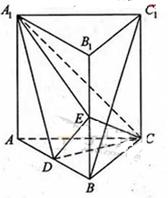
(Ⅰ)證明:BC1//平面A1CD;
(Ⅱ)設AA1=AC=CB=2,AB=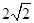 ,求三棱錐C一A1DE的體積.
,求三棱錐C一A1DE的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,斜三棱柱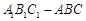 中,側面
中,側面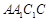
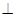 底面ABC,底面ABC是邊長為2的等邊三角形,側面
底面ABC,底面ABC是邊長為2的等邊三角形,側面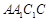 是菱形,
是菱形,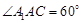 ,E、F分別是
,E、F分別是 、AB的中點.
、AB的中點.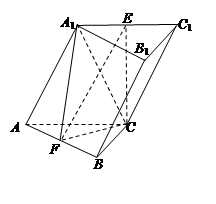
求證:(1)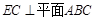 ;
;
(2)求三棱錐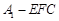 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖是一個直三棱柱被削去一部分后的幾何體的直觀圖與三視圖中的側視圖、俯視圖.在直觀圖中,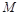 是
是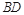 的中點.又已知側視圖是直角梯形,俯視圖是等腰直角三角形,有關數(shù)據(jù)如圖所示.
的中點.又已知側視圖是直角梯形,俯視圖是等腰直角三角形,有關數(shù)據(jù)如圖所示.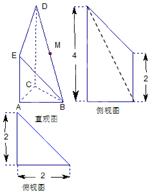
(Ⅰ)求證:EM∥平面ABC;
(Ⅱ)求出該幾何體的體積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com