
已知數列{an}是等差數列,a2=6,a5=12,數列{bn}的前n項和是Sn,且Sn+ bn=1.
bn=1.
(1)求數列{an}的通項公式.
(2)求證:數列{bn}是等比數列.
(3)記cn=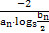 ,{cn}的前n項和為Tn,若Tn<
,{cn}的前n項和為Tn,若Tn<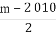 對一切n∈N*都成立,求最小正整數m.
對一切n∈N*都成立,求最小正整數m.
(1) an=2n+2 (2)見解析 (3) 2012
【解析】(1)設{an}的公差為d,則a2=a1+d,a5=a1+4d.
∵a2=6,a5=12,∴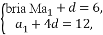
解得:a1=4,d=2.∴an=4+2(n-1)=2n+2.
(2)當n=1時,b1=S1,由S1+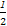 b1=1,得b1=
b1=1,得b1=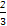 .
.
當n≥2時,∵Sn=1-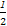 bn,Sn-1=1-
bn,Sn-1=1-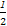 bn-1,
bn-1,
∴Sn-Sn-1=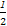 (bn-1-bn),即bn=
(bn-1-bn),即bn=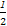 (bn-1-bn).
(bn-1-bn).
∴bn=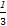 bn-1.
bn-1.
∴{bn}是以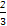 為首項,
為首項,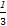 為公比的等比數列.
為公比的等比數列.
(3)由(2)可知:bn=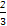 ·(
·(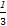 )n-1=2·(
)n-1=2·(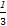 )n.
)n.
∴cn=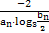 =
=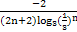 =
=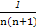 =
=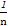 -
-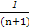 ,
,
∴Tn=(1-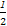 )+(
)+(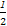 -
-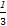 )+(
)+(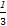 -
-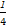 )+…+(
)+…+(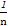 -
-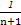 )=1-
)=1-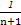 <1,
<1,
由已知得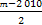 ≥1,∴m≥2012,
≥1,∴m≥2012,
∴最小正整數m=2012.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十第五章第一節練習卷(解析版) 題型:選擇題
在數列{an}中,a1=1,anan-1=an-1+(-1)n(n≥2,n∈N*),則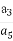 的值是( )
的值是( )
(A)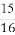 (B)
(B)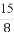 (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十五第六章第一節練習卷(解析版) 題型:選擇題
若 <
< <0,則下列不等式:①
<0,則下列不等式:①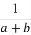 <
<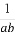 ;②|a|+b>0;③a-
;②|a|+b>0;③a- >b-
>b- ;④lna2>lnb2中,正確的是( )
;④lna2>lnb2中,正確的是( )
(A)①④ (B)②③ (C)①③ (D)②④
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十五第六章第一節練習卷(解析版) 題型:選擇題
已知a,b為實數,則“a>b>1”是“ <
< ”的( )
”的( )
(A)充分不必要條件 (B)必要不充分條件
(C)充分必要條件 (D)既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十二第五章第三節練習卷(解析版) 題型:選擇題
在正項等比數列{an}中,a1,a19分別是方程x2-10x+16=0的兩根,則a8·a10·a12等于( )
(A)16(B)32(C)64(D)256
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十九第六章第五節練習卷(解析版) 題型:選擇題
已知f(x+1)= ,f(1)=1(x∈N*),猜想f(x)的表達式為( )
,f(1)=1(x∈N*),猜想f(x)的表達式為( )
(A)f(x)=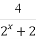 (B)f(x)=
(B)f(x)=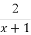
(C)f(x)=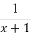 (D)f(x)=
(D)f(x)=
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十一第五章第二節練習卷(解析版) 題型:填空題
已知奇函數f(x)是定義在R上的增函數,數列{xn}是一個公差為2的等差數列,且滿足f(x8)+f(x9)+f(x10)+f(x11)=0,則x2012的值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com