|
|
|
某車間分批生產某種產品,每批的生產準備費用為800元.若每批生產x件,則平均倉儲時間為 ,且每件產品每天的倉儲費用為1元.為使平均到每件產品的生產準備費用 ,且每件產品每天的倉儲費用為1元.為使平均到每件產品的生產準備費用
與倉儲費用之和最小,每批應生產產品
|
| [ ] |
A. |
60件
|
B. |
80件
|
C. |
100件
|
D. |
120件
|
|
|
練習冊系列答案
相關習題
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
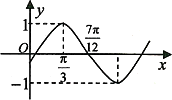
已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,-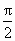 <φ< <φ<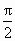 )的部分圖象如圖所示,則y=f(x)的圖象可由函數y=sinx的圖象(縱坐標不變)作下述變換得到 )的部分圖象如圖所示,則y=f(x)的圖象可由函數y=sinx的圖象(縱坐標不變)作下述變換得到
|
| [ ] |
A. |
先把各點的橫坐標縮短到原來的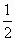 倍,再向右平移 倍,再向右平移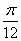 個單位 個單位
|
B. |
先把各點的橫坐標伸長到原來的2倍,再向右平移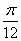 個單位 個單位
|
C. |
先把各點的橫坐標縮短到原來的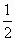 倍,再向右平移 倍,再向右平移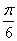 個單位 個單位
|
D. |
先把各點的橫坐標伸長到原來的2倍,再向左平移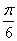 個單位 個單位
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
“lgx,lgy,lgz成等差數列”是“y2=xz”成立的
|
| [ ] |
A. |
充分非必要條件;
|
B. |
必要非充分條件;
|
C. |
充要條件
|
D. |
既非充分也非必要條件
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
如圖,△ABC是直角三角形,∠BAC=30°,BM⊥AC交AC于點M,EA⊥平面ABC,FC∥EA,AC=2BC=4,EA=3,FC=1.
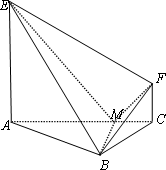
(1)證明:EM⊥BF;
(2)求平面BEF與平面ABC所成的銳二面角的余弦值.
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
如圖所示的是一個算法的流程圖,已知a1=3,輸出的結果為7,則a2的值是
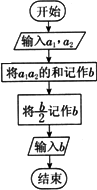
|
| [ ] |
A. |
9
|
B. |
10
|
C. |
11
|
D. |
12
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
若實數x,y滿足不等式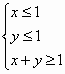 ,則 ,則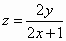 的取值范圍是________; 的取值范圍是________;
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
如圖所示為一個幾何體的直觀圖、三視圖(其中正視圖為直角梯形,俯視圖為正方形,側視圖為直角三角形,尺寸如圖所示).


(1)求四棱錐P-ABCD的體積;
(2)證明:BD∥平面PEC;
(3)若G為BC上的動點,求證:AE⊥PG.
|
|
|
查看答案和解析>>
科目:高中數學
來源:
題型:單選題
對于非空實數集A,記A*={y|?x∈A,y≥x}.設非空實數集合M、P滿足:M⊆P,且若x>1,則x∉P.現給出以下命題:
①對于任意給定符合題設條件的集合M、P,必有P*⊆M*;
②對于任意給定符合題設條件的集合M、P,必有M*∩P≠∅;
③對于任意給定符合題設條件的集合M、P,必有M∩P*=∅;
④對于任意給定符合題設條件的集合M、P,必存在常數a,使得對任意的b∈M*,恒有a+b∈P*.其中正確的命題是( )
查看答案和解析>>
