
直線l與球O有且只有一個公共點P,從直線l出發的兩個半平面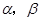 截球O的兩個截面圓的半徑分別為1和
截球O的兩個截面圓的半徑分別為1和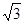 .若二面角
.若二面角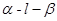 的平面角為150°,則球O的表面積為
的平面角為150°,則球O的表面積為
A. | B.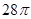 | C.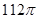 | D.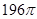 |
C
解析試題分析:欲求球O的表面積,只需求出球O的半徑,根據題意OP長即球O的半徑,再根據球心與截面圓圓心連線垂直截面圓,可考慮連接球心與兩個截面圓圓心,利用得到的圖形中的一些邊角關系,求出R,再利用球的表面積公式即可求出球O的表面積.
解:設平面α,β截球O的兩個截面圓的圓心分別為A,B,
連接PA,PB,與球交點為C,D根據題意在四邊形OAPB中,∠APB=150°,∠OAP=∠OBP=90°
∴∠AOB=30°,PA=1,PB=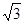 ,那么小圓的直徑分別是2,和2
,那么小圓的直徑分別是2,和2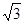 ,那么結合角∠APB=150°,運用余弦定理得到得到為CD=2
,那么結合角∠APB=150°,運用余弦定理得到得到為CD=2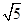 ,而球的半徑就是三角形PAB的外接圓的半徑,則利用正弦定理可知為球的半徑為2
,而球的半徑就是三角形PAB的外接圓的半徑,則利用正弦定理可知為球的半徑為2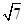 ,因此球的表面積為
,因此球的表面積為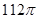 ,故選C.
,故選C.
考點:球的表面積
點評:本題考查了球的截面圓的性質,以及二面角的平面角的找法,綜合性較強,做題時要認真分析,找到聯系.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案科目:高中數學 來源: 題型:單選題
已知兩個不同的平面α, 和兩條不重合的直線m,n,則下列四種說法正確的為( )
和兩條不重合的直線m,n,則下列四種說法正確的為( )
A.若m∥n,n α,則m∥α α,則m∥α |
| B.若m⊥n,m⊥α,則n∥α |
C.若m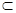 α,n α,n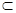  ,α∥ ,α∥ ,則m,n為異面直線 ,則m,n為異面直線 |
D.若α⊥ ,m⊥α,n⊥ ,m⊥α,n⊥ ,則m⊥n ,則m⊥n |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
設α,β為不重合的平面,m,n為不重合的直線,則下列命題正確的是( )
A.若m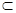 α,n α,n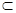 β,m∥n,則α∥β β,m∥n,則α∥β |
| B.若n⊥α,n⊥β,m⊥β,則m⊥α |
| C.若m∥α,n∥β,m⊥n,則α⊥β |
| D.若α⊥β,n⊥β,m⊥n,則m⊥α |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com