
圖是某市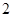 月
月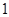 日至
日至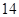 日的空氣質量指數趨勢圖,空氣質量指數(
日的空氣質量指數趨勢圖,空氣質量指數(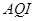 )小于
)小于 表示空氣質量優良,空氣質量指數大于
表示空氣質量優良,空氣質量指數大于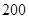 表示空氣重度污染,某人隨機選擇
表示空氣重度污染,某人隨機選擇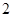 月
月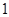 日至
日至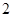 月
月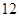 日中的某一天到達該市,并停留
日中的某一天到達該市,并停留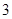 天.
天.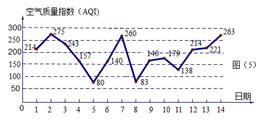
(1)求此人到達當日空氣質量優良的概率;
(2)求此人停留期間至多有1天空氣重度污染的概率.
(1)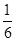 ;(2)
;(2)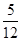 .
.
解析試題分析:(1)從圖中找出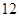 天內空氣質量優良的天數,從而確定此人到達當日空氣質量優良的概率;(2)將問題分為兩種:一種是沒有空氣質量重度污染,另一種是只有一天空氣質量重度污染,并從圖中找出相應的天數,從而確定題中涉及事件的概率.
天內空氣質量優良的天數,從而確定此人到達當日空氣質量優良的概率;(2)將問題分為兩種:一種是沒有空氣質量重度污染,另一種是只有一天空氣質量重度污染,并從圖中找出相應的天數,從而確定題中涉及事件的概率.
試題解析:(1)在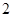 月
月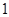 日至
日至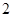 月
月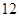 日這
日這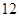 天中,只有
天中,只有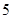 日、
日、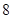 日共
日共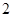 天的空氣質量優良,所以此人到達當日空氣質量優良的概率
天的空氣質量優良,所以此人到達當日空氣質量優良的概率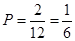 ;
;
(2)根據題意,事件“此人在該市停留期間至多有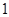 天空氣重度污染”,即“此人到達該市停留期間
天空氣重度污染”,即“此人到達該市停留期間 天空氣重度污染或僅有
天空氣重度污染或僅有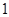 天空氣重度污染”.
天空氣重度污染”.
“此人在該市停留期間 天空氣重度污染”等價于“此人到達該市的日期是
天空氣重度污染”等價于“此人到達該市的日期是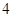 日或
日或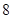 日或
日或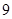 日”.其概率為
日”.其概率為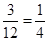 ,
,
“此人在該市停留期間僅有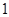 天空氣重度污染”等價于“此人到達該市的日期是
天空氣重度污染”等價于“此人到達該市的日期是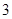 日或
日或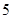 日或
日或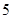 日或
日或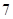 日或
日或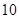 日”.其概率為
日”.其概率為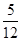 ,
,
所以此人停留期間至多有 天空氣重度污染的概率為
天空氣重度污染的概率為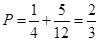 .
.
考點:古典概型


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:解答題
甲、乙兩名運動員參加“選拔測試賽”,在相同條件下,兩人5次測試的成績(單位:分)記錄如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用莖葉圖表示這兩組數據;.
(2)現要從中選派一名運動員參加比賽,你認為選派誰參賽更好?說明理由(不用計算);
(3)若將頻率視為概率,對運動員甲在今后三次測試成績進行預測,記這三次成績高于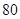 分的次數為
分的次數為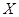 ,求
,求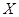 的分布列和數學期望
的分布列和數學期望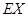 ..
..
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
爸爸和亮亮用4張撲克牌(方塊2,黑桃4,黑桃5,梅花5)玩游戲,他倆將撲克牌洗勻后,背面朝上放置在桌面上,爸爸先抽,亮亮后抽,抽出的牌不放回.
(1)若爸爸恰好抽到了黑桃4.
①請把右面這種情況的樹形圖繪制完整;
②求亮亮抽出的牌的牌面數字比4大的概率.
(11)爸爸、亮亮約定,若爸爸抽到的牌的牌面數字比亮亮的大,則爸爸勝;反之,則亮亮贏,你認為這個游戲是否公平?如果公平,請說明理由,如果不公平,更換一張撲克牌使游戲公平.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個袋中裝有形狀大小完全相同的球9個,其中紅球3個,白球6個,每次隨機取1個,直到取出3次紅球即停止.
(1)從袋中不放回地取球,求恰好取4次停止的概率P1;
(2)從袋中有放回地取球.
①求恰好取5次停止的概率P2;
②記5次之內(含5次)取到紅球的個數為 ,求隨機變量
,求隨機變量 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某飲料公司招聘了一名員工,現對其進行一項測試,以便確定工資級別.公司準備了兩種不同的飲料共8杯,其顏色完全相同,并且其中4杯為A飲料,另外4杯為B飲料,公司要求此員工一一品嘗后,從8杯飲料中選出4杯A飲料,若4杯都選對,則月工資定為3500元;若4杯選對3杯,則月工資定為2 800元,否則月工資定為2100元,令X表示此人選對A飲料的杯數,假設此人對A和B兩種飲料沒有鑒別能力.
(1)求X的分布列:
(2)求此員工月工資的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲乙兩個同學進行定點投籃游戲,已知他們每一次投籃投中的概率均為 ,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.
,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.
(1)求甲同學至少有4次投中的概率;
(2)求乙同學投籃次數 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解甲、乙兩個快遞公司的工作狀況,假設同一個公司快遞員的工作狀況基本相同,現從甲、乙兩公司各隨機抽取一名快遞員,并從兩人某月(30天)的快遞件數記錄結果中隨機抽取10天的數據,制表如下:
| 甲公司某員工A | | 乙公司某員工B | ||||||||||||
| 3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
| | | | | | | 0 | 1 | 4 | 4 | 2 | 2 | 2 | | |
 (單位:元),求
(單位:元),求 的分布列和數學期望;
的分布列和數學期望;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知一個矩形由三個相同的小矩形拼湊而成(如圖所示),用三種不同顏色給3個小矩形涂色,每個小矩形只涂一種顏色,求:
(1)3個矩形都涂同一顏色的概率;
(2)3個小矩形顏色都不同的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知直線l1:x-2y-1=0,直線l2:ax-by+1=0,其中a,b∈{1,2,3,4,5,6}.
(1) 求直線l1與l2相交的概率;
(2) 求直線l1與l2的交點位于第一象限的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com