
為了解甲、乙兩個快遞公司的工作狀況,假設同一個公司快遞員的工作狀況基本相同,現從甲、乙兩公司各隨機抽取一名快遞員,并從兩人某月(30天)的快遞件數記錄結果中隨機抽取10天的數據,制表如下:
| 甲公司某員工A | | 乙公司某員工B | ||||||||||||
| 3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
| | | | | | | 0 | 1 | 4 | 4 | 2 | 2 | 2 | | |
 (單位:元),求
(單位:元),求 的分布列和數學期望;
的分布列和數學期望;(1)平均數為36,眾數為33.(2)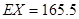
(3)甲公司4860元,乙公司4965元
136 147 154 189 203 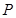
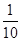
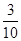
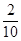
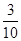
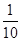
解析試題分析:(1)由平均數計算公式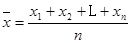 得:
得: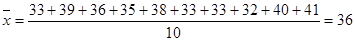 ,出現得最多的數是33.(2)先計算出隨機變量取值集合,當投遞件數為34時,
,出現得最多的數是33.(2)先計算出隨機變量取值集合,當投遞件數為34時,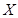 =136元;當投遞件數為36時,
=136元;當投遞件數為36時,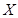 =147元;當投遞件數為37時,
=147元;當投遞件數為37時,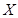 =154元;當投遞件數為42時,
=154元;當投遞件數為42時,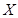 =189元;當投遞件數為44時,
=189元;當投遞件數為44時,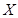 =1203元;再分別求出其概率,最后利用數學期望公式
=1203元;再分別求出其概率,最后利用數學期望公式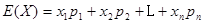 求出
求出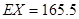 (3)甲公司被抽取員工該月收入為
(3)甲公司被抽取員工該月收入為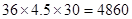 元,乙公司被抽取員工該月收入為
元,乙公司被抽取員工該月收入為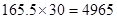 元.
元.
試題解析:解:
(1)甲公司員工A投遞快遞件數的平均數為36,眾數為33. 2分
(2)設 為乙公司員工B投遞件數,則
為乙公司員工B投遞件數,則
當 =34時,
=34時,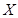 =136元,當
=136元,當 >35時,
>35時,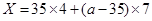 元,
元, 的可能取值為136,147,154,189,203 4分
的可能取值為136,147,154,189,203 4分
{說明:X取值都對給4分,若計算有錯,在4分基礎上錯1個扣1分,4分扣完為止 的分布列為:
的分布列為:
9分
136 147 154 189 203 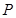
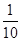
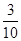
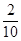
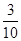
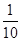
{說明:每個概率值給1分,不化簡不扣分,隨機變量值計算錯誤的此處不再重復扣分}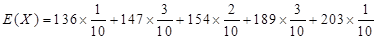
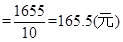 11分
11分
(3)根據圖中數據,可估算甲公司被抽取員工該月收入4860元,乙公司被抽取員工該月收入4965元. 13分
考點:分布列,數學期望


科目:高中數學 來源: 題型:解答題
某校高三(1)班共有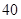 名學生,他們每天自主學習的時間全部在
名學生,他們每天自主學習的時間全部在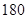 分鐘到
分鐘到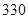 分鐘之間,按他們學習時間的長短分
分鐘之間,按他們學習時間的長短分 個組統計,得到如下頻率分布表:
個組統計,得到如下頻率分布表:
| 組別 | 分組 | 頻數 | 頻率 |
| 第一組 | 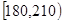 | | 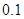 |
| 第二組 | 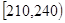 |  | 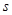 |
| 第三組 | 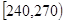 | 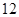 | 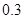 |
| 第四組 | 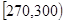 | 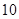 | 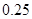 |
| 第五組 | 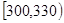 | | 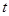 |
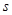 ,
,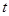 的值;
的值;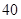 名學生中抽取
名學生中抽取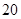 名進行研究,問應抽取多少名第一組的學生?
名進行研究,問應抽取多少名第一組的學生?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
圖是某市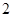 月
月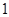 日至
日至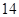 日的空氣質量指數趨勢圖,空氣質量指數(
日的空氣質量指數趨勢圖,空氣質量指數(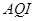 )小于
)小于 表示空氣質量優良,空氣質量指數大于
表示空氣質量優良,空氣質量指數大于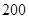 表示空氣重度污染,某人隨機選擇
表示空氣重度污染,某人隨機選擇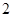 月
月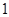 日至
日至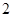 月
月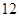 日中的某一天到達該市,并停留
日中的某一天到達該市,并停留 天.
天.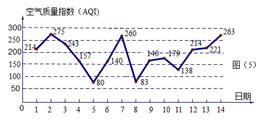
(1)求此人到達當日空氣質量優良的概率;
(2)求此人停留期間至多有1天空氣重度污染的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校舉行中學生“日常生活小常識”知識比賽,比賽分為初賽和復賽兩部分,初賽采用選手從備選題中選一題答一題的方式進行;每位選手最多有5次答題機會,選手累計答對3題或答錯3題即終止比賽,答對3題者直接進入復賽,答錯3題者則被淘汰.已知選手甲答對每個題的概率均為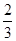 ,且相互間沒有影響.
,且相互間沒有影響.
(1)求選手甲進入復賽的概率;
(2)設選手甲在初賽中答題的個數為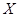 ,試求
,試求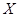 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
年齡在60歲(含60歲)以上的人稱為老齡人,某地區老齡人共有35萬,隨機調查了該地區700名老齡人的健康狀況,結果如下表:
| 健康指數 | 2 | 1 | 0 | -1 |
| 60歲至79歲的人數 | 250 | 260 | 65 | 25 |
| 80歲及以上的人數 | 20 | 45 | 20 | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某單位從一所學校招收某類特殊人才.對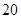 位已經選拔入圍的學生進行運動協調能力和邏輯思維能力的測試,其測試結果如下表:
位已經選拔入圍的學生進行運動協調能力和邏輯思維能力的測試,其測試結果如下表:
 | 一般 | 良好 | 優秀 |
| 一般 |  |  |  |
| 良好 | 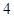 |  |  |
| 優秀 |  |  | 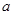 |
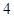 人.由于部分數據丟失,只知道從這
人.由于部分數據丟失,只知道從這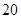 位參加測試的學生中隨機抽取一位,抽到邏輯思維能力優秀的學生的概率為
位參加測試的學生中隨機抽取一位,抽到邏輯思維能力優秀的學生的概率為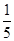 .
.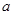 ,
, 的值;
的值; 位,求其中至少有一位邏輯思維能力優秀的學生的概率.
位,求其中至少有一位邏輯思維能力優秀的學生的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某大廈的一部電梯從底層出發后只能在第18,19,20層可以停靠,若該電梯在底層載有5位乘客,且每位乘客在這三層的每一層下電梯的概率均為 ,用X表示這5位乘客在第20層下電梯的人數,求隨機變量X的分布列.
,用X表示這5位乘客在第20層下電梯的人數,求隨機變量X的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
全國第十二屆全國人民代表大會第二次會議和政協第十二屆全國委員會第二次會議,2014年3月在北京開幕.期間為了了解國企員工的工資收入狀況,從108名相關人員中用分層抽樣方法抽取若干人組成調研小組,有關數據見下表:(單位:人)
| | 相關人數 | 抽取人數 |
| 一般職工 | 63 | 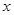 |
| 中層 | 27 | 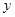 |
| 高管 | 18 | 2 |
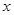 ,
,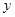 ;
;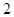 人,求這二人都來自中層的概率.
人,求這二人都來自中層的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工藝廠開發一種新工藝品,頭兩天試制中,該廠要求每位師傅每天制作10件,該廠質檢部每天從每位師傅制作的10件產品中隨機抽取4件進行檢查,若發現有次品,則當天該師傅的產品不能通過.已知李師傅第一天、第二天制作的工藝品中分別有2件、1件次品.
(1)求兩天中李師傅的產品全部通過檢查的概率;
(2)若廠內對師傅們制作的工藝品采用記分制,兩天全不通過檢查得0分,通過1天、2天分別得1分、2分,求李師傅在這兩天內得分的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com