
(08年福州質檢理)(12分)
已知![]() 上不相同的兩個點,l是弦AB的垂直平分線.
上不相同的兩個點,l是弦AB的垂直平分線.
(1)當![]() +
+![]() 取何值時,可使拋物線的焦點F與原點O到直線l的距離相等?證明你的結論;
取何值時,可使拋物線的焦點F與原點O到直線l的距離相等?證明你的結論;
(2)當直線l的斜充為1時,求l在y軸上截距的取值范圍.
解析:(1)由已知,拋物線![]() ,焦點F的坐標為F(0,1)………………1分
,焦點F的坐標為F(0,1)………………1分
當l與y軸重合時,顯然符合條件,此時![]() ……………………3分
……………………3分
當l不與y軸重合時,要使拋物線的焦點F與原點O到直線l的距離相等,當且僅當直線l通過點(![]() )設l的斜率為k,則直線l的方程為
)設l的斜率為k,則直線l的方程為![]()
由已知可得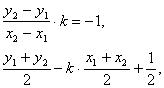 即
即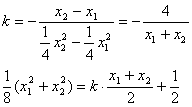 ………5分
………5分
解得![]() 無意義.
無意義.
因此,只有![]() 時,拋物線的焦點F與原點O到直線l的距離相等.……7分
時,拋物線的焦點F與原點O到直線l的距離相等.……7分
(2)由已知可設直線l的方程為![]() ……………………8分
……………………8分
則AB所在直線為![]() ……………………9分
……………………9分
代入拋物線方程![]() ………………①
………………①
∴![]() 的中點為
的中點為![]()
代入直線l的方程得:![]() ………………10分
………………10分
又∵對于①式有:![]()
解得m>-1,
∴![]()
∴l在y軸上截距的取值范圍為(3,+![]() )……………………12分
)……………………12分


 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源: 題型:
(08年福州質檢理)(12分)
某公司以每噸10萬元的價格銷售某種化工產品,每年可售出該產品1000噸,若將該產品每噸的價格上漲x%,則每年的銷售數量將減少mx%,其中m為正常數.
(1)當![]() 時,該產品每噸的價格上漲百分之幾,可使銷售的總金額最大?
時,該產品每噸的價格上漲百分之幾,可使銷售的總金額最大?
(2)如果漲價能使銷售總金額增加,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年福州質檢理)(12分)
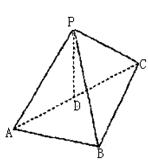
如圖,P―ABC中,D是AC的中點,PA=PB=PC=![]()
(1)求證:PD⊥平面ABC;
(2)求二面角P―AB―C的大小;
(3)求AB的中點E到平面PBC的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com