
已知直線 的參數方程為
的參數方程為 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, 軸的正半軸為極軸建立極坐標系,圓
軸的正半軸為極軸建立極坐標系,圓 的極坐標方程為
的極坐標方程為 .求:
.求:
(1)求圓 的直角坐標方程;
的直角坐標方程;
(2)若 是直線
是直線 與圓面
與圓面 ≤
≤ 的公共點,求
的公共點,求 的取值范圍.
的取值范圍.
(1)
 .(2)
.(2) .
.
解析試題分析:(1)先將 利用兩角差的正弦公式展開,方程兩邊在乘以
利用兩角差的正弦公式展開,方程兩邊在乘以 ,利用直角坐標與極坐標互化公式即可將極坐標方程互為直角坐標方程;(2)先將直線方程化為普通方程互化,求出直線與圓的交點A、B坐標,作出直線
,利用直角坐標與極坐標互化公式即可將極坐標方程互為直角坐標方程;(2)先將直線方程化為普通方程互化,求出直線與圓的交點A、B坐標,作出直線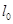 :
: =0,平移直線
=0,平移直線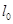 ,結合圖形,找出直線z=
,結合圖形,找出直線z= 與線段AB相交時,z取最大值與最小值點,求出z的最大值與最小值,即可求出
與線段AB相交時,z取最大值與最小值點,求出z的最大值與最小值,即可求出 的取值范圍.
的取值范圍.
試題解析:(1)因為圓 的極坐標方程為
的極坐標方程為
所以
又
所以

所以圓 的直角坐標方程為:
的直角坐標方程為:
 . 6分
. 6分
(2)『解法1』:
設
由圓 的方程
的方程



所以圓 的圓心是
的圓心是 ,半徑是
,半徑是
將 代入
代入 得
得
又直線 過
過 ,圓
,圓 的半徑是
的半徑是 ,由題意有:
,由題意有:
所以
即 的取值范圍是
的取值范圍是 . 14分
. 14分
『解法2』:
直線 的參數方程化成普通方程為:
的參數方程化成普通方程為:
由
解得 ,
,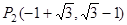
∵ 是直線
是直線 與圓面
與圓面 的公共點,
的公共點,
∴點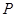 在線段
在線段 上,
上,
∴ 的最大值是
的最大值是 ,
,
最小值是
∴ 的取值范圍是
的取值范圍是 . 14分
. 14分
考點:極坐標方程與直角坐標方程互化;參數方程與普通方程互化互化;直線與圓的位置關系;數形結合想


科目:高中數學 來源: 題型:解答題
直角坐標系xOy中,以原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的方程為
 ,直線
,直線 方程為
方程為 (t為參數),直線
(t為參數),直線 與C的公共點為T.
與C的公共點為T.
(1)求點T的極坐標;
(2)過點T作直線 ,
, 被曲線C截得的線段長為2,求直線
被曲線C截得的線段長為2,求直線 的極坐標方程.
的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
將圓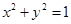 上每一點的橫坐標保持不變,縱坐標變為原來的2倍,得曲線C.
上每一點的橫坐標保持不變,縱坐標變為原來的2倍,得曲線C.
(1)寫出C的參數方程;
(2)設直線 與C的交點為
與C的交點為 ,以坐標原點為極點,x軸正半軸為極坐標建立極坐標系,求過線段
,以坐標原點為極點,x軸正半軸為極坐標建立極坐標系,求過線段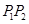 的中點且與
的中點且與 垂直的直線的極坐標方程.
垂直的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知曲線 的極坐標方程是
的極坐標方程是 ,以極點為原點,極軸為
,以極點為原點,極軸為 軸正半軸,建立平面直角坐標系,兩坐標系中取相同的長度單位.
軸正半軸,建立平面直角坐標系,兩坐標系中取相同的長度單位.
(1)寫出曲線 的普通方程,并說明它表示什么曲線;
的普通方程,并說明它表示什么曲線;
(2)過點
 作傾斜角為
作傾斜角為 的直線
的直線 與曲線
與曲線 相交于
相交于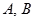 兩點,求線段
兩點,求線段 的長度和
的長度和 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知在平面直角坐標系 中,圓
中,圓 的方程為
的方程為 .以原點
.以原點 為極點,以
為極點,以 軸正半軸為極軸,且與直角坐標系取相同的單位長度,建立極坐標系,直線
軸正半軸為極軸,且與直角坐標系取相同的單位長度,建立極坐標系,直線 的極坐標方程為
的極坐標方程為 .
.
(1)求直線 的直角坐標方程和圓
的直角坐標方程和圓 的參數方程;
的參數方程;
(2)求圓 上的點到直線
上的點到直線 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在直角坐標系中,以原點為極點, 軸的正半軸為極軸建立極坐標系,兩種坐標系取相同單位長度.已知曲線
軸的正半軸為極軸建立極坐標系,兩種坐標系取相同單位長度.已知曲線 過點
過點 的直線
的直線 的參數方程為
的參數方程為 (t為參數). (1)求曲線C與直線
(t為參數). (1)求曲線C與直線 的普通方程;(2)設曲線C經過伸縮變換
的普通方程;(2)設曲線C經過伸縮變換 得到曲線
得到曲線 ,若直線
,若直線 與曲線
與曲線 相切,求實數
相切,求實數 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com