
若數(shù)軸上不同的兩點(diǎn) 分別與實(shí)數(shù)
分別與實(shí)數(shù) 對應(yīng),則線段
對應(yīng),則線段 的中點(diǎn)
的中點(diǎn) 與實(shí)數(shù)
與實(shí)數(shù) 對應(yīng),由此結(jié)論類比到平面得,若平面上不共線的三點(diǎn)
對應(yīng),由此結(jié)論類比到平面得,若平面上不共線的三點(diǎn) 分別與二元實(shí)數(shù)對
分別與二元實(shí)數(shù)對 對應(yīng),則
對應(yīng),則 的重心
的重心 與 對應(yīng).
與 對應(yīng).
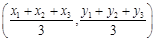
解析試題分析:根據(jù)題意,由于數(shù)軸上不同的兩點(diǎn) 分別與實(shí)數(shù)
分別與實(shí)數(shù) 對應(yīng),則線段
對應(yīng),則線段 的中點(diǎn)
的中點(diǎn) 與實(shí)數(shù)
與實(shí)數(shù) 對應(yīng),由此結(jié)論類比到平面得,若平面上不共線的三點(diǎn)
對應(yīng),由此結(jié)論類比到平面得,若平面上不共線的三點(diǎn) 分別與二元實(shí)數(shù)對
分別與二元實(shí)數(shù)對 對應(yīng),則
對應(yīng),則 的重心
的重心 與三個(gè)數(shù)的算術(shù)平均數(shù)有關(guān),即
與三個(gè)數(shù)的算術(shù)平均數(shù)有關(guān),即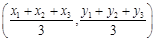 項(xiàng)對應(yīng)。
項(xiàng)對應(yīng)。
考點(diǎn):類比推理
點(diǎn)評:解決的關(guān)鍵是理解類比推理的性質(zhì),然后找到性質(zhì)的相似之處,進(jìn)而得到結(jié)論,屬于基礎(chǔ)題。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
平面上有 條直線, 這
條直線, 這 條直線任意兩條不平行, 任意三條不共點(diǎn), 記這
條直線任意兩條不平行, 任意三條不共點(diǎn), 記這 條直線將平面分成
條直線將平面分成 部分, 則
部分, 則 ___________,
___________,  時(shí),
時(shí), _________________.)(用
_________________.)(用 表示).
表示).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
類比平面內(nèi) “垂直于同一條直線的兩條直線互相平行”的性質(zhì),可推出空間下列結(jié)論:①垂直于同一條直線的兩條直線互相平行;②垂直于同一個(gè)平面的兩條直線互相平行;③垂直于同一條直線的兩個(gè)平面互相平行;④垂直于同一個(gè)平面的兩個(gè)平面互相平行.則正確結(jié)論的序號是
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
在 中,兩直角邊分別為
中,兩直角邊分別為 、
、 ,設(shè)
,設(shè) 為斜邊上的高,則
為斜邊上的高,則 ,由此類比:三棱錐
,由此類比:三棱錐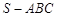 中的三條側(cè)棱
中的三條側(cè)棱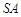 、
、 、
、 兩兩垂直,且長度分別為
兩兩垂直,且長度分別為 、
、 、
、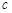 ,設(shè)棱錐底面
,設(shè)棱錐底面 上的高為
上的高為 ,則 .
,則 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
在平面幾何里,已知直角三角形ABC中,角C為
 ,AC=b,BC=a,運(yùn)用類比方法探求空間中三棱錐的有關(guān)結(jié)論:
,AC=b,BC=a,運(yùn)用類比方法探求空間中三棱錐的有關(guān)結(jié)論:
有三角形的勾股定理,給出空間中三棱錐的有關(guān)結(jié)論:________
若三角形ABC的外接圓的半徑為 ,給出空間中三棱錐的有關(guān)結(jié)論:________
,給出空間中三棱錐的有關(guān)結(jié)論:________
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
我們把平面內(nèi)與直線垂直的非零向量稱為直線的法向量,在平面直角坐標(biāo)系中,利用求動點(diǎn)軌跡方程的方法,可以求出過點(diǎn)A(-3,4),且法向量為 =(1,-2)的直線(點(diǎn)法式)方程為:1×(x+3)+(-2)×(y-4)=0,化簡得x-2y+11=0.類比以上方法,在空間直角坐標(biāo)系o-xyz中,經(jīng)過點(diǎn)A(1,2,3)且法向量為
=(1,-2)的直線(點(diǎn)法式)方程為:1×(x+3)+(-2)×(y-4)=0,化簡得x-2y+11=0.類比以上方法,在空間直角坐標(biāo)系o-xyz中,經(jīng)過點(diǎn)A(1,2,3)且法向量為 =(-1,-2,1)的平面的方程為____________ .
=(-1,-2,1)的平面的方程為____________ .
(化簡后用關(guān)于x,y,z的一般式方程表示)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
把1,3,6,10,15,21, 這些數(shù)叫做三角形,這是因?yàn)檫@些數(shù)目的點(diǎn)可以排成一個(gè)正三角形(如下面),則第七個(gè)三角形數(shù)是 .
這些數(shù)叫做三角形,這是因?yàn)檫@些數(shù)目的點(diǎn)可以排成一個(gè)正三角形(如下面),則第七個(gè)三角形數(shù)是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
下列表述:①綜合法是執(zhí)因?qū)Чǎ虎诰C合法是順推法;③分析法是執(zhí)果索因法;④分析法是間接證法;⑤反證法是逆推法。正確的語句有是______(填序號)。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com