
(本小題13分) 如圖所示, PQ為平面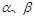 的交線, 已知二面角
的交線, 已知二面角 為直二面角,
為直二面角, 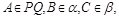
 , ∠BAP=45°.
, ∠BAP=45°.
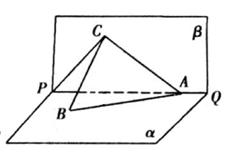
(1)證明: BC⊥PQ;
(2)設(shè)點C在平面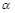 內(nèi)的射影為點O, 當(dāng)k取何值時, O在平面ABC內(nèi)的射影G恰好為△ABC的重心?
內(nèi)的射影為點O, 當(dāng)k取何值時, O在平面ABC內(nèi)的射影G恰好為△ABC的重心?
(3)當(dāng) 時, 求二面角B-AC-P的大小.
時, 求二面角B-AC-P的大小.
(1)證明見解析
(2)k=1
(3)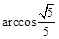
【解析】(1)在平面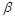 內(nèi)過點C作CE⊥PQ于點E, 由題知點E與點A不重合,
連接EB.
內(nèi)過點C作CE⊥PQ于點E, 由題知點E與點A不重合,
連接EB.
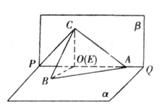
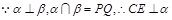 ,
即點C在平面
,
即點C在平面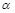 內(nèi)的射影為點E,
內(nèi)的射影為點E,
所以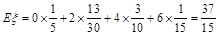 .
.
又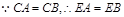 .
.
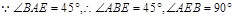 ,
故 BE⊥PQ, 又
,
故 BE⊥PQ, 又
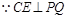 ,
,  ,
,
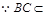 平面EBC, 故BC⊥PQ.
平面EBC, 故BC⊥PQ.
(2)由(1)知, O點即為E點, 設(shè)點F是O在平面ABC內(nèi)的射影, 連 接BF并延長交AC于點D, 由題意可知, 若F是△ABC的重心, 則點D為AC的中點.
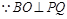 , 平面角
, 平面角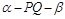 為直二面角,
為直二面角, 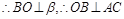 , 由三垂線定理可知AC⊥BF, 即AC⊥BD,
, 由三垂線定理可知AC⊥BF, 即AC⊥BD, 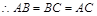 ,
即k=1;反之, 當(dāng)k=1時, 三棱錐O—ABC為正三棱錐, 此時, 點O在平面ABC內(nèi)的射影恰好為△ABC的重心.
,
即k=1;反之, 當(dāng)k=1時, 三棱錐O—ABC為正三棱錐, 此時, 點O在平面ABC內(nèi)的射影恰好為△ABC的重心.
(3)由(2)知, 可以O為原點, 以OB、OA、OC所在的直線為x軸、y軸、z軸建立空間直角坐標(biāo)系O—xyz(如圖所示)
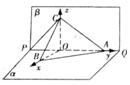
不妨設(shè)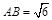 , 在Rt△OAB中, ∠ABO=∠BAO=45°,
所以BO=AO=
, 在Rt△OAB中, ∠ABO=∠BAO=45°,
所以BO=AO=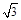 , 由CA=CB=kAB且
, 由CA=CB=kAB且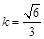 得, AC=2,
得, AC=2, 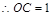 ,
則
,
則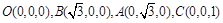 .
.
所以
設(shè)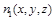 是平面ABC的一個法向量, 由
是平面ABC的一個法向量, 由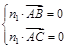 得
得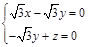
取x=1, 得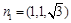
易知 是平面
是平面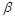 的一個法向量,
的一個法向量,
設(shè)二面角B-AC-P的平面角為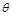 , 所以
, 所以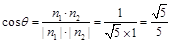 , 由圖可知,
, 由圖可知,
二面角B-AC-P的大小為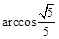 .
.


科目:高中數(shù)學(xué) 來源:2014屆湖北武漢部分重點中學(xué)高二上學(xué)期期末考試文科數(shù)學(xué)卷(解析版) 題型:解答題
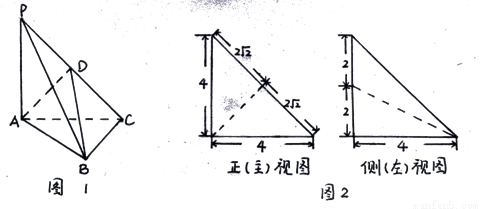
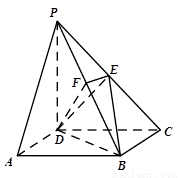
(本小題13分)如圖1,在三棱錐P—ABC中,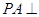 平面ABC,
平面ABC,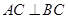 ,D為側(cè)棱PC上一點,它的正(主)視圖和側(cè)(左)視圖如圖2所示。
,D為側(cè)棱PC上一點,它的正(主)視圖和側(cè)(左)視圖如圖2所示。
(1)證明: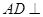 平面PBC;
平面PBC;
(2)求三棱錐D—ABC的體積;
(3)在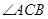 的平分線上確定一點Q,使得
的平分線上確定一點Q,使得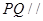 平面ABD,并求此時PQ的長。
平面ABD,并求此時PQ的長。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆福建省高二上學(xué)期期中考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
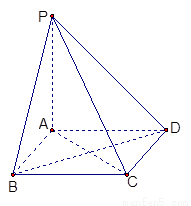
(本小題13分)如圖,棱錐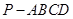 的底面
的底面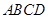 是矩形,
是矩形,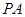 ⊥平面
⊥平面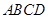 ,
,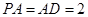 ,
,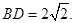
(1)求證: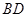 ⊥平面
⊥平面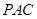 ;
;
(2)求二面角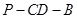 的大小;
的大小;
(3)求點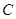 到平面
到平面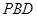 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆安徽宿松縣復(fù)興中學(xué)高一第二學(xué)期第三次月考數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題13分)
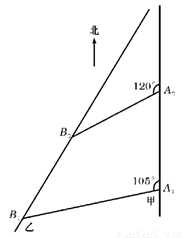
如圖,甲船以每小時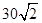 海里的速度向正北方向航行,乙船按固定方向勻速直線航行,當(dāng)甲船位于
海里的速度向正北方向航行,乙船按固定方向勻速直線航行,當(dāng)甲船位于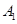 處時,乙船位于甲船的北偏西
處時,乙船位于甲船的北偏西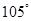 的方向
的方向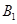 處,此時兩船相距20海里.當(dāng)甲船航行20分鐘到達
處,此時兩船相距20海里.當(dāng)甲船航行20分鐘到達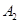 處時,乙船航行到甲船的北偏西
處時,乙船航行到甲船的北偏西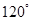 方向的
方向的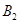 處,此時兩船相距
處,此時兩船相距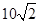 海里,問乙船每小時航行多少海里?
海里,問乙船每小時航行多少海里?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年北京市東城區(qū)示范校高三第二學(xué)期綜合練習(xí)數(shù)學(xué)文卷 題型:解答題
(本小題13分)如圖,在四棱錐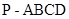 中,
中,
底面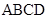 是矩形,側(cè)棱PD⊥底面
是矩形,側(cè)棱PD⊥底面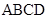 ,
,
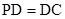 ,
,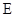 是
是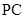 的中點,作
的中點,作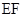 ⊥
⊥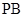 交
交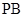 于點
于點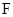 .
.
(1)證明: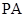 ∥平面
∥平面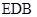 ;
;
(2)證明: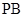 ⊥平面
⊥平面 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
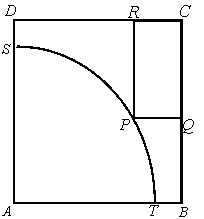
(本小題13分)如圖![]() 是一塊邊長為100米的正方形地皮,其中
是一塊邊長為100米的正方形地皮,其中![]() 是一半徑為90米的扇形小山,
是一半徑為90米的扇形小山,![]() 是弧
是弧![]() 上一點,其余都是平地,現(xiàn)一開發(fā)商想在平地上建造一個有邊落在
上一點,其余都是平地,現(xiàn)一開發(fā)商想在平地上建造一個有邊落在![]() 與
與![]() 上的長方形停車場
上的長方形停車場![]() ,求長方形停車場的最大面積和最小面積。(請將結(jié)果精確到個位)【提示:
,求長方形停車場的最大面積和最小面積。(請將結(jié)果精確到個位)【提示:![]() 】
】
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com