
 數列an的前n項和為Sn(n∈N*),點(n,Sn)均在函數y=f(x)的圖象上,
數列an的前n項和為Sn(n∈N*),點(n,Sn)均在函數y=f(x)的圖象上, ,證明
,證明 .
. n2+
n2+ n,可得an=Sn-Sn-1=n+1,并驗證a1即可;
n,可得an=Sn-Sn-1=n+1,并驗證a1即可;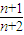 +
+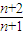 >2,得c1+c2+…+cn>2n;由cn=
>2,得c1+c2+…+cn>2n;由cn= +
+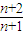 =2+
=2+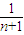 -
-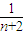 ,得c1+c2+…+cn=2n+(
,得c1+c2+…+cn=2n+( -
- +
+ -
- +…+
+…+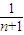 -
-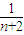 )=2n+
)=2n+ -
-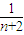 <2n+
<2n+ ;即證.
;即證.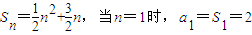 ,
,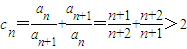 ,∴c1+c2+…+cn>2n;
,∴c1+c2+…+cn>2n;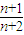 +
+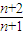 =2+
=2+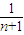 -
-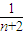 ,∴c1+c2+…+cn=2n+(
,∴c1+c2+…+cn=2n+( -
- +
+ -
- +…+
+…+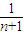 -
-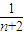 )=2n+
)=2n+ -
-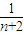 <2n+
<2n+ ;
; .
.

科目:高中數學 來源: 題型:解答題
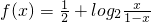 .
.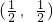 成中心對稱;
成中心對稱;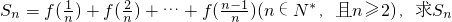 ;
;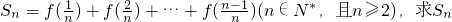 ,數列{an}的前n項和為Tn.若Tn<λ(Sn+1+1)對一切n∈N*都成立,求λ的取值范圍.
,數列{an}的前n項和為Tn.若Tn<λ(Sn+1+1)對一切n∈N*都成立,求λ的取值范圍.查看答案和解析>>
科目:高中數學 來源: 題型:
(08年聊城市四模文)(14分)已知函數![]() +
+![]() 數列{an}的首項為1,前n項和為Sn,且
數列{an}的首項為1,前n項和為Sn,且![]() ,在函數f(x)的圖像上.
,在函數f(x)的圖像上.
(1)證明:數列{an}是等差數列;
(2)若b=4,向量![]() 、
、![]() ,動點M滿足
,動點M滿足![]() ,點N是曲線
,點N是曲線![]() 上的動點,求|MN|的最小值.
上的動點,求|MN|的最小值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年安徽省巢湖市高三(上)質量檢測數學試卷(理科)(解析版) 題型:解答題
 .
.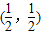 成中心對稱;
成中心對稱;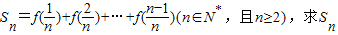 ;
;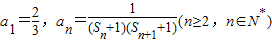 ,數列{an}的前n項和為Tn.若Tn<λ(Sn+1+1)對一切n∈N*都成立,求λ的取值范圍.
,數列{an}的前n項和為Tn.若Tn<λ(Sn+1+1)對一切n∈N*都成立,求λ的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com