
已知函數![]() (a,c∈R,a>0,b是自然數)是奇函數,f(x)有最大值
(a,c∈R,a>0,b是自然數)是奇函數,f(x)有最大值![]() ,且f(1)>
,且f(1)>![]() .
.
(1)求函數f(x)的解析式;
(2)是否存在直線l與y=f(x)的圖象交于P、Q兩點,并且使得P、Q兩點關于點(1,0)對稱,若存在,求出直線l的方程,若不存在,說明理由.
(1)f(x)=![]() (2)P (
(2)P (![]() )或(
)或(![]() ),Q(
),Q(![]() )或Q(
)或Q(![]() ),過P、Q的直線l的方程: x–4y–1=0即為所求.
),過P、Q的直線l的方程: x–4y–1=0即為所求.
(1)∵f(x)是奇函數
∴f(–x)=–f(x),即
![]()
∴–bx+c=–bx–c ∴c=0
∴f(x)=![]()
由a>0,b是自然數得當x≤0時,f(x)≤0,
當x>0時,f(x)>0
∴f(x)的最大值在x>0時取得.
∴x>0時,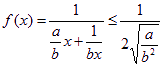
當且僅當![]()
即![]() 時,f(x)有最大值
時,f(x)有最大值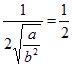
∴![]() =1,∴a=b2 ①
=1,∴a=b2 ①
又f(1)>![]() ,∴
,∴![]() >
>![]() ,∴5b>2a+2 ②
,∴5b>2a+2 ②
把①代入②得2b2–5b+2<0解得![]() <b<2
<b<2
又b∈N,∴b=1,a=1,∴f(x)=![]()
(2)設存在直線l與y=f(x)的圖象交于P、Q兩點,且P、Q關于點(1,0)對稱,
P(x0,y0)則Q(2–x0,–y0),∴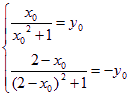 ,消去y0,得x02–2x0–1=0
,消去y0,得x02–2x0–1=0
解之,得x0=1±![]() ,
,
∴P點坐標為(![]() )或(
)或(![]() )
)
進而相應Q點坐標為Q(![]() )或Q(
)或Q(![]() ).
).
過P、Q的直線l的方程: x–4y–1=0即為所求.
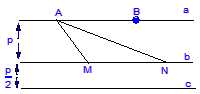


 優百分課時互動系列答案
優百分課時互動系列答案 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案科目:高中數學 來源: 題型:
| x+1 |
| 2x-1 |
| a |
| x |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省寧波市柴橋中學高三(上)10月月考數學試卷(理科)(解析版) 題型:解答題
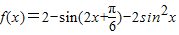 ,x∈R
,x∈R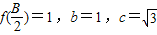 ,求a的值.
,求a的值.查看答案和解析>>
科目:高中數學 來源:2014屆寧夏高三年級第一次月考理科數學試卷(解析版) 題型:選擇題
已知函數 定義在R上的奇函數,當
定義在R上的奇函數,當 時,
時, ,給出下列命題:
,給出下列命題:
①當 時,
時, ②函數
②函數 有2個零點
有2個零點
③ 的解集為
的解集為 ④
④ ,都有
,都有
其中正確命題個數是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中數學 來源:2014屆甘肅天水一中高二下學期期末考試理科數學試卷(解析版) 題型:選擇題
已知函數 (k∈R),若函數
(k∈R),若函數 有三個零點,則實數k的取值范圍是( )
有三個零點,則實數k的取值范圍是( )
(A)k≤2 (B)-1<k<0
(C)-2≤k<-1 (D)k≤-2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com