
在平面直角坐標系中,已知點 ,點
,點 在直線
在直線 :
: 上運動,過點
上運動,過點 與
與 垂直的直線和線段
垂直的直線和線段 的垂直平分線相交于點
的垂直平分線相交于點 .
.
(1)求動點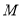 的軌跡
的軌跡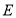 的方程;
的方程;
(2)過(1)中的軌跡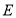 上的定點
上的定點
 作兩條直線分別與軌跡
作兩條直線分別與軌跡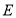 相交于
相交于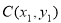 ,
, 兩點.試探究:當直線
兩點.試探究:當直線 ,
, 的斜率存在且傾斜角互補時,直線
的斜率存在且傾斜角互補時,直線 的斜率是否為定值?若是,求出這個定值;若不是,說明理由.
的斜率是否為定值?若是,求出這個定值;若不是,說明理由.
(1) 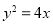 (2) 當直線
(2) 當直線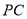 ,
,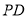 的斜率存在且傾斜角互補時,直線
的斜率存在且傾斜角互補時,直線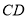 的斜率為定值
的斜率為定值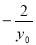
【解析】
試題分析:(1)由線段垂直平分線的性質知, 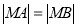 ,所以動點
,所以動點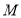 的軌跡
的軌跡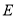 是以
是以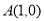 為焦點,直線
為焦點,直線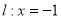 為準線的拋物線.易知其標準方程為
為準線的拋物線.易知其標準方程為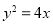 .
.
設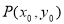 、
、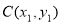 ,
,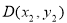 ,可由點差法求出
,可由點差法求出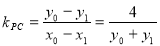 ,
,
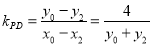 ,
,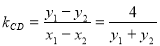
由直線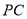 ,
,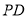 的傾斜角互補,得
的傾斜角互補,得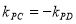
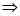
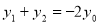
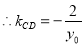 定值
定值
試題解析:(1)依題意,得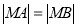 1分
1分
∴動點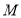 的軌跡
的軌跡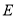 是以
是以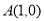 為焦點,直線
為焦點,直線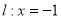 為準線的拋物線 3分
為準線的拋物線 3分
∴動點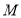 的軌跡
的軌跡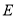 的方程為
的方程為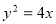 4分
4分
(2)∵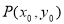 、
、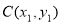 ,
,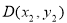 在拋物線
在拋物線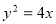 上
上
∴  5分
5分
由①-②得,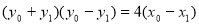
∴直線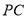 的斜率為
的斜率為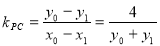 7分
7分
同理可得,直線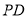 的斜率為
的斜率為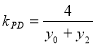 9分
9分
∴當直線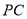 ,
,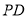 的傾斜角互補時,有
的傾斜角互補時,有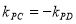
即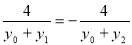
∴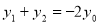 11分
11分
由②-③得,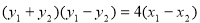
∴直線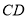 的斜率為
的斜率為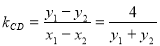 ④ 13分
④ 13分
將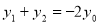 代入④,得
代入④,得 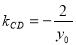
∴當直線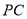 ,
,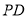 的斜率存在且傾斜角互補時,直線
的斜率存在且傾斜角互補時,直線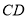 的斜率為定值
的斜率為定值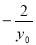 14分
14分
考點:1、拋物線的定義和標準方程;2、點差法的應用.


科目:高中數學 來源:2015屆廣東惠州高二第一學期期末考試文科數學試卷(解析版) 題型:選擇題
已知事件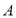 與事件
與事件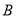 發生的概率分別為
發生的概率分別為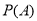 、
、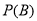 ,有下列命題:
,有下列命題:
①若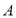 為必然事件,則
為必然事件,則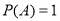 ; ②若
; ②若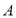 與
與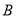 互斥,則
互斥,則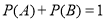 ;
;
③若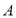 與
與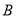 互斥,則
互斥,則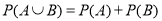 .
.
其中真命題有( )個
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源:2015屆廣東臺山高二第一學期期末測試理科數學試卷(解析版) 題型:解答題
已知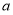 ,
,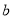 ,
,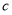 分別是
分別是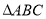 的三個內角
的三個內角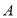 ,
,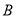 ,
,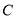 所對的邊,且
所對的邊,且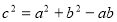 .
.
(1)求角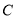 的值;
的值;
(2)若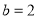 ,
, 的面積
的面積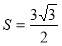 ,求
,求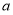 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2015屆廣東臺山高二第一學期期末測試理科數學試卷(解析版) 題型:選擇題
甲、乙兩人同時從圖書館走向教室,甲一半路程步行,一半路程跑步;乙一半時間步行,一半時間跑步,若兩人步行、跑步的速度一樣,則先到教室的是
A.甲 B.乙 C.甲、乙同時到達 D.無法確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com