(本小題滿分14分)
如圖5所示,在三棱錐
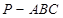
中,
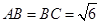
,平面
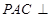
平面
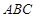
,
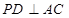
于點
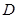
,
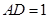
,
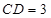
,
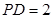
.
(1)求三棱錐
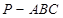
的體積;
(2)證明△
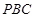
為直角三角形.

(1)證明:因為平面
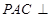
平面
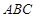
,平面

平面

,

平面

,
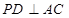
,
所以

平面
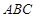
.
記

邊上的中點為

,在△

中,因為

,
所以

.
因為
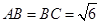
,

,
所以

.
所以△

的面積

.
因為
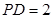
,
所以三棱錐
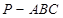
的體積


.
(2)證法1:因為


,所以△

為直角三角形.
因為

,
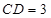
,

所以

.
連接

,在

△

中,
因為

,

,

,
所以

.
由(1)知

平面
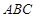
,又

平面
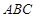
,
所以


.
在

△
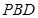
中,因為
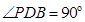
,

,

,
所以

.
在

中,因為

,

,

,
所以

.
所以

為直角三角形.
證法2:連接

,在

△

中,因為

,

,

,
所以

.
在△

中,
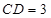
,

,

,
所以

,所以

.
由(1)知

平面
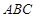
,
因為
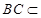
平面
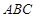
,
所以

.
因為

,
所以

平面
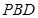
.
因為

平面
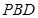
,所以

.
所以

為直角三角形.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
本小題滿分14分)
如圖,在直三棱柱

中,

,

,

,點

、

分別是

、

的中點.
(Ⅰ)求證:

平面

;
(Ⅱ)證明:平面

平面

;
(Ⅲ)求多面體A
1B
1C
1BD的體積V.

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
、(滿分14分)如圖,正方體
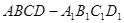
的棱長為2,E為AB的中點.
(Ⅰ)求證:
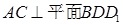
(Ⅱ)求異面直線BD
1與AD所成角的余弦值。
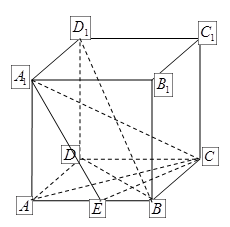
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
一個平面內(nèi)有無數(shù)條直線平行于另一個平面,那么這兩個平面
| A.一定平行 | B.一定相交 | C.平行或相交 | D.一定重合 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若

是互不相同的空間直線,

是不重合的平面,則下列命題中為真命題的是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知
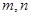
表示不同直線,
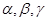
表示不同平面.下列四個命題中真命題為( )
①


②
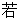
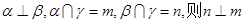
③
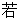
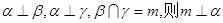
④
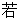
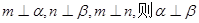
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本題滿分14分)
如下圖(圖1)等腰梯形PBCD,A為PD上一點,且AB⊥PD,AB=BC,AD=2BC,沿著AB折疊使得二面角P-AB-D為
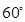
的二面角,連結(jié)PC、PD,在AD上取一點E使得3AE=ED,連結(jié)PE得到如下圖(圖2)的一個幾何體.
(1)求證:平面PAB
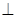
平面PCD;
(2)求PE與平面PBC所成角的正弦值.
查看答案和解析>>

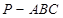 中,
中,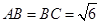 ,平面
,平面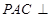 平面
平面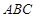 ,
,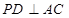 于點
于點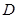 ,
, 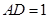 ,
,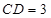 ,
,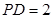 .
.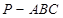 的體積;
的體積;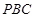 為直角三角形.
為直角三角形.
 中,
中, ,
, ,
, ,點
,點 、
、 分別是
分別是 、
、 的中點.
的中點.  平面
平面 ;
;  平面
平面 ;
;
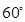 的二面角,連結(jié)PC、PD,在AD上取一點E使得3AE=ED,連結(jié)PE得到如下圖(圖2)的一個幾何體.
的二面角,連結(jié)PC、PD,在AD上取一點E使得3AE=ED,連結(jié)PE得到如下圖(圖2)的一個幾何體. 平面PCD;
平面PCD;