
本著健康、低碳的生活理念,租自行車騎游的人越來越多。某自行車租車點的收費標準是每車每次租車時間不超過兩小時免費,超過兩小時的部分每小時收費標準為2元(不足1小時的部分按1小時計算)。有甲乙兩人相互獨立來該租車點租車騎游(各租一車一次),設甲、乙不超過兩小時還車的概率分別為 ;兩小時以上且不超過三小時還車的概率分別為
;兩小時以上且不超過三小時還車的概率分別為 ;兩人租車時間都不會超過四小時。
;兩人租車時間都不會超過四小時。
(1)求出甲、乙兩人所付租車費用相同的概率;
(2)設甲、乙兩人所付的租車費用之和為隨機變量 ,求
,求 的分布列與數學期望
的分布列與數學期望
科目:高中數學 來源: 題型:解答題
由于某高中建設了新校區,為了交通方便要用三輛通勤車從老校區把教師接到新校區.已知從新校區到老校區有兩條公路,汽車走一號公路堵車的概率為 ,不堵車的概率為
,不堵車的概率為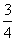 ;汽車走二號公路堵車的概率為p,不堵車的概率為1-p,若甲、乙兩輛汽車走一號公路,丙汽車由于其他原因走二號公路,且三輛車是否堵車相互之間沒有影響.
;汽車走二號公路堵車的概率為p,不堵車的概率為1-p,若甲、乙兩輛汽車走一號公路,丙汽車由于其他原因走二號公路,且三輛車是否堵車相互之間沒有影響.
(Ⅰ)若三輛汽車中恰有一輛汽車被堵的概率為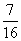 ,求走二號公路堵車的概率;
,求走二號公路堵車的概率;
(Ⅱ)在(Ⅰ)的條件下,求三輛汽車中被堵車輛的個數ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在某校高三學生的數學校本課程選課過程中,規定每位同學只能選一個科目。已知某班第一小組與第二小組各 有六位同學選擇科目甲或科 目乙,情況如下表:
| | 科目甲 | 科目乙 | 總計 |
| 第一小組 | 1 | 5 | 6 |
| 第二小組 | 2 | 4 | 6 |
| 總計 | 3 | 9 | 12 |
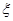 為選出的4個人中選科目甲的人數,求
為選出的4個人中選科目甲的人數,求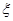 的分布列和數學期望.
的分布列和數學期望.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了防止受到核污染的產品影響我國民眾的身體健康,要求產品進入市場前必須進行兩輪核放射檢測,只有兩輪都合格才能進行銷售。已知某產品第一輪檢測不合格的概率為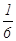 ,第二輪檢測不合格的概率為
,第二輪檢測不合格的概率為 ,兩輪檢測是否合格相互沒有影響。
,兩輪檢測是否合格相互沒有影響。
(1)求該產品不能銷售的概率
(2)如果產品可以銷售,則每件產品可獲利40元;如果產品不能銷售,則每件產品虧損80元(即獲利-80元)。已知一箱中有4件產品,記可銷售的產品數為X,求X的分布列,并求一箱產品獲利的均值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一家化妝品公司于今年三八節期間在某社區舉行了為期三天的“健康使用化妝品知識講座”.每位社區居民可以在這三天中的任意一天參加任何一個討論,也可以放棄任何一個講座(規定:各個講座達到預先設定的人數時稱為滿座).統計數據表明,各個講座各天滿座的概率如下表:
| | 洗發水講座 | 洗面奶講座 | 護膚霜講座 | 活顏營養講座 | 面膜使用講座 |
| 3月8日 | 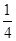 | 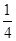 | 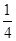 | 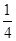 |  |
| 3月9日 |  |  |  |  | 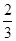 |
| 3月10日 | 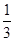 | 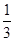 | 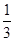 | 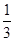 | 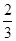 |
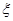 ,求隨機變量
,求隨機變量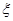 的分布列和數學期望.
的分布列和數學期望.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某某種飲料每箱6聽,如果其中有兩聽不合格產品.
(1)質檢人員從中隨機抽出1聽,檢測出不合格的概率多大?;
(2)質檢人員從中隨機抽出2聽,設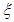 為檢測出不合格產品的聽數,求
為檢測出不合格產品的聽數,求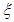 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某商場有獎銷售中,購滿100元商品得1張獎券,多購多得。每1000張獎券為一個開獎單位,其中含特等獎1個,一等獎10個,二等獎50個。設1張獎券中特等獎、一等獎、二等獎的事件分別為A、B、C,求:
(1)P(A),P(B),P(C);
(2)1張獎券的中獎概率;
(3)1張獎券不中特等獎且不中一等獎的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)
從裝有大小相同的2個紅球和6個白球的袋子中,每摸出2個球為一次試驗,直到摸出的球中有紅球(不放回),則試驗結束.
(Ⅰ)求第一次試驗恰摸到一個紅球和一個白球概率;
(Ⅱ)記試驗次數為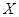 ,求
,求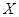 的分布列及數學期望
的分布列及數學期望 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com