
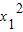
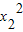 =1,對應的x1、x2不唯一,故y=x-2不是K函數,得①不正確;對于函數y=2x,若f(x1)f(x2)=1得
=1,對應的x1、x2不唯一,故y=x-2不是K函數,得①不正確;對于函數y=2x,若f(x1)f(x2)=1得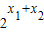 =1,即x1+x2=0,所以x2=-x1,可得x2存在且唯一得函數y=2x是K函數,故②正確;對于③,因為函數y=lnx有零點,可得當x1=1時,不存在x2滿足f(x1)f(x2)=1成立,故函數y=lnx不是K函數,所以③不正確.由此可得本題的答案.
=1,即x1+x2=0,所以x2=-x1,可得x2存在且唯一得函數y=2x是K函數,故②正確;對于③,因為函數y=lnx有零點,可得當x1=1時,不存在x2滿足f(x1)f(x2)=1成立,故函數y=lnx不是K函數,所以③不正確.由此可得本題的答案.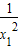 •
•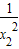 =1,即
=1,即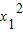
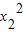 =1,
=1,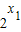 •
•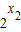 =
=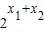 =1,即x1+x2=0,
=1,即x1+x2=0,

 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com