有驅蟲藥1618和1573各3杯,從中隨機取出3杯稱為一次試驗(假定每杯被取到的概率相等),將1618全部取出稱為試驗成功.
(1)求一次試驗成功的概率.
(2)求恰好在第3次試驗成功的概率(要求將結果化為最簡分數).
(1)試驗一次就成功的概率為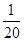
； (2)
.
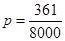解析試題分析：(1)將6杯驅蟲藥逐一編號，再將從中任選3杯的所有結果共一一列舉出來，得不同選法共有20種，而選到的3杯都是1618的選法只有1種，由古典概型概率的求法可得試驗一次就成功的概率為.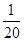
(2)恰好在第3次試驗成功相當于前兩次試驗都沒成功，第3次才成功.由于成功的概率為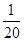，所以一次試驗沒有成功的概率為
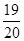，三次相乘即得所求概率.
試題解析：(1)從6杯中任選3杯,將不同選法一一列舉，共有20種選法，而選到的3杯都是1618的選法只有1種,從而試驗一次就成功的概率為.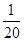
(2)相當于前兩次試驗都沒成功,第3次才成功,故概率為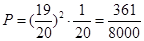
.
考點：古典概型.
小學教材全測系列答案
小學數學口算題卡脫口而出系列答案
優秀生應用題卡口算天天練系列答案
浙江之星課時優化作業系列答案科目：高中數學 來源： 題型：解答題
某商店試銷某種商品20天，獲得如下數據：
| 日銷售量（件） | 0 | 1 | 2 | 3 |
| 頻數 | 1 | 5 | 9 | 5 |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
甲向靶子A射擊兩次，乙向靶子射擊一次.甲每次射擊命中靶子的概率為0.8，命中得5分；乙命中靶子的概率為0.5，命中得10分.
（1）求甲、乙二人共命中一次目標的概率；
（2）設X為二人得分之和，求X的分布列和期望.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某籃球隊與其他6支籃球隊依次進行6場比賽，每場均決出勝負，設這支籃球隊與其他籃球隊比賽勝場的事件是獨立的，并且勝場的概率是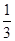
.
(1)求這支籃球隊首次勝場前已經負了兩場的概率；
(2)求這支籃球隊在6場比賽中恰好勝了3場的概率；
(3)求這支籃球隊在6場比賽中勝場數的期望和方差．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
A高校自主招生設置了先后三道程序：部分高校聯合考試、本校專業考試、本校面試．在每道程序中，設置三個成績等級：優、良、中．若考生在某道程序中獲得“中”，則該考生在本道程序中不通過，且不能進入下面的程序．考生只有全部通過三道程序，自主招生考試才算通過．某中學學生甲參加A高校自主招生考試，已知該生在每道程序中通過的概率均為
，每道程序中得優、良、中的概率分別為p1、
、p2.
(1)求學生甲不能通過A高校自主招生考試的概率；
(2)設X為學生甲在三道程序中獲優的次數，求X的概率分布及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某中學為豐富教工生活，國慶節舉辦教工趣味投籃比賽，有
、
兩個定點投籃位置，在點投中一球得2分，在點投中一球得3分.其規則是：按先后再的順序投
籃.教師甲在和點投中的概率分別是
，且在、兩點投中與否相互獨立.
（1）若教師甲投籃三次，試求他投籃得分X的分布列和數學期望；
（2）若教師乙與甲在A、B點投中的概率相同，兩人按規則各投三次，求甲勝乙的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某課程考核分理論與實驗兩部分進行，每部分考核成績只記“合格”與“不合格”，兩部分考核都是“合格”，則該課程考核“合格”，若甲、乙、丙三人在理論考核中合格的概率分別為0.9,0.8,0.7，在實驗考核中合格的概率分別為0.8,0.7,0.9，所有考核是否合格相互之間沒有影響．
(1)求甲、乙、丙三人在理論考核中至少有兩人合格的概率；
(2)求這三個人該課程考核都合格的概率(結果保留三位小數)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
.