
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
在某校教師趣味投籃比賽中,比賽規則是: 每場投6個球,至少投進4個球且最后2個球都投進者獲獎;否則不獲獎. 已知教師甲投進每個球的概率都是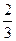 .
.
(1)記教師甲在每場的6次投球中投進球的個數為X,求X的分布列及數學期望;
(2)求教師甲在一場比賽中獲獎的概率;
(3)已知教師乙在某場比賽中,6個球中恰好投進了4個球,求教師乙在這場比賽中獲獎的概率;教師乙在這場比賽中獲獎的概率與教師甲在一場比賽中獲獎的概率相等嗎?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩人各擲一次骰子(均勻的正方體,六個面上分別為1,2,3,4,5,6點),所得點數分別為x,y
(1)求x<y的概率;
(2)求5<x+y<10的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
小明家訂了一份報紙,寒假期間他收集了每天報紙送達時間的數據,并繪制成頻率分布直方圖,如圖所示.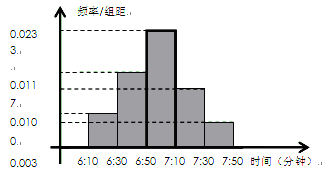
(1)根據圖中的數據信息,求出眾數 和中位數
和中位數 (精確到整數分鐘);
(精確到整數分鐘);
(2)小明的父親上班離家的時間 在上午
在上午 之間,而送報人每天在
之間,而送報人每天在 時刻前后半小時內把報紙送達(每個時間點送達的可能性相等),求小明的父親在上班離家前能收到報紙(稱為事件
時刻前后半小時內把報紙送達(每個時間點送達的可能性相等),求小明的父親在上班離家前能收到報紙(稱為事件 )的概率.
)的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學在高一開設了數學史等4門不同的選修課,每個學生必須選修,且只能從中選一門.該校高一的3名學生甲、乙、丙對這4門不同的選修課的興趣相同.
(1)求3個學生選擇了3門不同的選修課的概率;
(2)求恰有2門選修課這3個學生都沒有選擇的概率;
(3)設隨機變量X為甲、乙、丙這三個學生選修數學史這門課的人數,求X的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙、丙三名射擊運動員射中目標的概率分別為 、a、a(0<a<1),三人各射擊一次,擊中目標的次數記為ξ.
、a、a(0<a<1),三人各射擊一次,擊中目標的次數記為ξ.
(1)求ξ的分布列及數學期望;
(2)在概率P(ξ=i)(i=0、1、2、3)中,若P(ξ=1)的值最大,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某選修課的考試按A級、B級依次進行,只有當A級成績合格時,才可繼續參加B級的考試.已知每級考試允許有一次補考機會,兩個級別的成績均合格方可獲得該選修課的合格證書.現某人參加這個選修課的考試,他A級考試成績合格的概率為 ,B級考試合格的概率為
,B級考試合格的概率為 .假設各級考試成績合格與否均互不影響.
.假設各級考試成績合格與否均互不影響.
(1)求他不需要補考就可獲得該選修課的合格證書的概率;
(2)在這個考試過程中,假設他不放棄所有的考試機會,記他參加考試的次數為 ,求
,求 的數學期望E
的數學期望E .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有驅蟲藥1618和1573各3杯,從中隨機取出3杯稱為一次試驗(假定每杯被取到的概率相等),將1618全部取出稱為試驗成功.
(1)求一次試驗成功的概率.
(2)求恰好在第3次試驗成功的概率(要求將結果化為最簡分數).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 、
、 兩個盒子中分別裝有標記為
兩個盒子中分別裝有標記為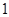 ,
, ,
, ,
, 的大小相同的四個小球,甲從
的大小相同的四個小球,甲從 盒中等可能地取出
盒中等可能地取出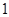 個球,乙從
個球,乙從 盒中等可能地取出
盒中等可能地取出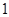 個球.
個球.
(1)用有序數對 表示事件“甲抽到標號為
表示事件“甲抽到標號為 的小球,乙抽到標號為
的小球,乙抽到標號為 的小球”,試寫出所有可能的事件;
的小球”,試寫出所有可能的事件;
(2)甲、乙兩人玩游戲,約定規則:若甲抽到的小球的標號比乙大,則甲勝;反之,則乙勝.你認為此規則是否公平?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com