
(本小題12分)某工廠有工人1000名,其中250名工人參加過短期培訓(稱為A類工人),另外750名工人參加過長期培訓(稱為B類工人).現用分層抽樣方法(按A類,B類分二層)從該工廠的工人中共抽查100名工人,調查他們的生產能力(生產能力指一天加工的零件數).從A類工人中抽查結果和從B類工人中的抽查結果分別如下表1和表2
表1:
|
生產能力分組 |
|
|
|
|
|
|
人數 |
4 |
8 |
|
5 |
3 |
表2:
|
生產能力分組 |
|
|
|
|
|
人數 |
6 |
y |
36 |
18 |
(1)先確定 ,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)(注意:本題請在答題卡上作圖)
,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)(注意:本題請在答題卡上作圖)

(2)分別估計 類工人和
類工人和 類工人生產能力的眾數、中位數和平均數。(精確到0.1)
類工人生產能力的眾數、中位數和平均數。(精確到0.1)
解:(1)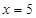 ;
; 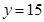 。頻率分布直方圖如下:
。頻率分布直方圖如下:
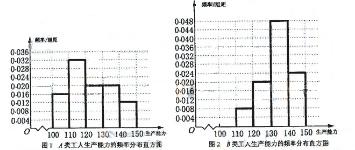
從直方圖可以判斷: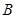 類工人中個體間的差異程度更小。
類工人中個體間的差異程度更小。
(2)A類工人生產能力的平均數、B類工人生產能力的平均數的估計值分別為123,133.8。
【解析】
試題分析:(1)根據隨機抽樣中各個個體被抽到的可能性均相等,可以得出甲、乙兩工人分別被抽到的概率,再根據獨立事件概率的計算公式求得結果;
(2)①利用分層抽樣的思想確定出A類工人和B類工人分別被抽查到的人數,然后根據統計表格利用方程確定出x,y的值,完成頻率分布直方圖,通過頻率分布直方圖判斷出A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小;
②利用頻率分布直方圖各組小長方形上端的中點橫坐標作為該組的生產能力估計值,各組的頻率值作為近似的概率值利用均值的計算公式估算出他們的生產能力平均數.
解:(1)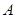 類工人中和
類工人中和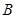 類工人中分別抽查25名和75名。由
類工人中分別抽查25名和75名。由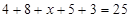 ,得
,得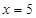 ;
;
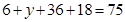 ,得
,得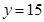 。
。
頻率分布直方圖如下:

從直方圖可以判斷: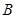 類工人中個體間的差異程度更小。
類工人中個體間的差異程度更小。
(2)A類工人生產能力的眾數、 B類工人生產能力的眾數的估計值為115,135;
A類工人生產能力的中位數、B類工人生產能力的中位數的估計值為121,134.6

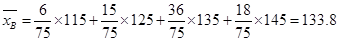 ,
,
A類工人生產能力的平均數、B類工人生產能力的平均數的估計值分別為123,133.8。
考點:本試題主要考查了統計的基本知識,考查用樣本估計總體的思想,考查隨機抽樣的基本思想和方法,分層抽樣的思想、相互獨立事件同時發生的概率的計算方法,考查頻率分布直方圖的繪畫、學生的畫圖、識圖能力,數據平均值的計算方法.
點評:易錯點就是對于均值的求解不知道如何結合圖像來求解。解決該試題的關鍵是理解分層抽樣法以及頻率分布直方圖和數據的平均值的的求解公式。


 高中必刷題系列答案
高中必刷題系列答案科目:高中數學 來源: 題型:
(本小題滿分12分)
某工廠有工人1000名,其中250名工人參加過短期培訓(稱為A類工人),另外750名工人參加過長期培訓(稱為B類工人),現用分層抽樣方法(按A類、B類分二層)從該工廠的工人中共抽查100名工人,調查他們的生產能力(此處生產能力指一天加工的零件數)。
(I)求甲、乙兩工人都被抽到的概率,其中甲為A類工人,乙為B類工人;
(II)從A類工人中的抽查結果和從B類工人中的抽插結果分別如下表1和表2.
表1:
生產能力分組 |
|
|
|
|
|
人數 | 4 | 8 |
| 5 | 3 |
表2:
生產能力分組 |
|
|
|
|
人數 | 6 | y | 36 | 18 |
(i)先確定x,y,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)

(ii)分別估計A類工人和B類工人生產能力的平均數,并估計該工廠工人的生產能力的平均數,同一組中的數據用該組區間的中點值作代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
(2009寧夏海南卷理)(本小題滿分12分)
某工廠有工人1000名, 其中250名工人參加過短期培訓(稱為A類工人),另外750名工人參加過長期培訓(稱為B類工人),現用分層抽樣方法(按A類、B類分二層)從該工廠的工人中共抽查100名工人,調查他們的生產能力(此處生產能力指一天加工的零件數)。
(I)求甲、乙兩工人都被抽到的概率,其中甲為A類工人,乙為B類工人;
(II)從A類工人中的抽查結果和從B類工人中的抽插結果分別如下表1和表2.
表1:
| 生產能力分組 |
|
|
|
|
|
| 人數 | 4 | 8 |
| 5 | 3 |
表2:
| 生產能力分組 |
|
|
|
|
| 人數 | 6 | y | 36 | 18 |
(i)先確定x,y,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)

(ii)分別估計A類工人和B類工人生產能力的平均數,并估計該工廠工人的生產能力的平均數,同一組中的數據用該組區間的中點值作代表)
查看答案和解析>>
科目:高中數學 來源:2012-2013學年遼寧沈陽二中等重點中學協作體高三領航高考預測(二)理數學卷(解析版) 題型:解答題
(本小題滿分12分)某品牌的汽車4S店,對最近100位采用分期付款的購車者進行統計,統計結果如下表所示:已知分3期付款的頻率為0.2,4S店經銷一輛該品牌的汽車,顧客分1期付款,其利潤為1萬元,分2期或3期付款其利潤為1.5萬元;分4期或5期付款,其利潤為2萬元,用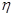 表示經銷一輛汽車的利潤。
表示經銷一輛汽車的利潤。
|
付款方工 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
|
頻數 |
40 |
20 |
|
10 |
|
(1)求上表中的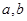 值;(2)若以頻率作為概率,求事件A:“購買該品牌汽車的3位顧客中,至多有1位采用3期付款”的頻率P(A);(3)求
值;(2)若以頻率作為概率,求事件A:“購買該品牌汽車的3位顧客中,至多有1位采用3期付款”的頻率P(A);(3)求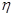 的分布列及數學期望E
的分布列及數學期望E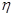 。
。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三五月模擬考試(一)理科數學試卷(解析版) 題型:解答題
(本小題滿分12分)某工廠生產甲、乙兩種產品,每種產品都是經過第一道和第二道工序加工而成,兩道工序的加工結果相互獨立,每道工序的加工結果均有 兩個等級.對每種產品,兩道工序的加工結果都為
兩個等級.對每種產品,兩道工序的加工結果都為 級時,產品為一等品,其余均為二等品。
級時,產品為一等品,其余均為二等品。
(1)已知甲、乙兩種產品每一道工序的加工結果為A級的概率如表一所示,分別求生產出的甲、乙產品為一等品的概率 ;
;



(2)已知一件產品的利潤如表二所示,用 分別表示一件甲、乙產品的利潤,在(1)的條件下,求
分別表示一件甲、乙產品的利潤,在(1)的條件下,求 的分布列及
的分布列及 ;
;
(3)已知生產一件產品需用的工人數和資金額如表三所示。該工廠有工人 名,可用資金
名,可用資金
 萬元。設
萬元。設 分別表示生產甲、乙產品的數量,在(2)的條件下,
分別表示生產甲、乙產品的數量,在(2)的條件下, 為何值時,
為何值時, 最大?最大值是多少?(解答時須給出圖示說明)
最大?最大值是多少?(解答時須給出圖示說明)
查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京市高三起點考試理科數學卷 題型:解答題
(本小題滿分12分)
某品牌的汽車4S店,對最近100位采用分期付款的購車者進行統計,統計結果如下表所示:已知分3期付款的頻率為0.2,4S店經銷一輛該品牌的汽車,顧客分1期付款,其利潤為1萬元,分2期或3期付款其利潤為1.5萬元;分4期或5期付款,其利潤為2萬元,用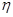 表示經銷一輛汽車的利潤。
表示經銷一輛汽車的利潤。
|
付款方工 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
|
頻數 |
40 |
20 |
|
10 |
|
(1)求上表中的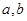 值;
值;
(2)若以頻率作為概率,求事件A:“購買該品牌汽車的3位顧客中,至多有1位采用3期付款”的頻率P(A);
(3)求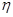 的分布列及數學期望E
的分布列及數學期望E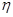 。
。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com