
某校高一某班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,(陰影部分為破壞部分)其可見部分如下,據此解答如下問題:


(Ⅰ)計算頻率分布直方圖中[80,90)間的矩形的高;
(Ⅱ)若要從分數在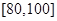 之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份的分數在
之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份的分數在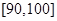 之間的概率;
之間的概率;
(Ⅲ)根據頻率分布直方圖估計這次測試的平均分.
(Ⅰ)0.016(Ⅱ)0.6(Ⅲ)73.8
解析試題分析:(Ⅰ)先由平率分布直方圖計算出分數在[50,60]間的頻率,由莖葉圖知:分數在
科目:高中數學
來源:
題型:填空題
從甲、乙兩品種的棉花中各抽測了25根棉花的纖維長度(單位:mm),結果如下:
科目:高中數學
來源:
題型:解答題
甲、乙二人參加知識競賽活動,組委會給他們準備了難、中、易三種題型,其中容易題兩道,分值各10分,中檔題一道,分值20分,難題一道,分值40分,二人需從4道題中隨機抽取一道題作答(所選題目可以相同)
科目:高中數學
來源:
題型:解答題
為了檢驗“喜歡玩手機游戲與認為作業多”是否有關系,某班主任對班級的30名學生進行了調查,得到一個2×2列聯表:
科目:高中數學
來源:
題型:解答題
巴西世界杯足球賽正在如火如荼進行.某人為了了解我校學生“通過電視收看世界杯”是否與性別有關,從全校學生中隨機抽取30名學生進行了問卷調查,得到了如下列聯表:
科目:高中數學
來源:
題型:解答題
假設關于某設備使用年限x(年)和所支出的維修費用y(萬元)有如下統計資料:
科目:高中數學
來源:
題型:解答題
青年歌手電視大賽共有10名選手參加,并請了7名評委,如圖所示的莖葉圖是7名評委給參加最后決賽的兩位選手甲、乙評定的成績,流程圖用來編寫程序統計每位選手的成績(各評委所給有效分數的平均值),試根據所給條件回答下列問題:
科目:高中數學
來源:
題型:解答題
某校高一某班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,其可見部分如下,據此解答如下問題:
科目:高中數學
來源:
題型:填空題
某校共有教師300人,其中高級教師90人,中級教師有150人.初級教師60人,為了了解教師的健康狀況,抽取一個容量為40的樣本,用分層抽樣的方法抽取高級教師、中級教師、初級教師的人數分別為 、 、 .
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
之間的頻數,算出全班人數,由莖葉圖知分數不在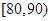 之間的人數,從而求出分數在
之間的人數,從而求出分數在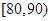 之間的人數即頻數,頻數除以總人數即為頻率,再除以組距即為矩形的高;(Ⅱ)設出分數在
之間的人數即頻數,頻數除以總人數即為頻率,再除以組距即為矩形的高;(Ⅱ)設出分數在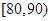 間的分數編號及分數在
間的分數編號及分數在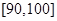 之間的分數編號,列出在
之間的分數編號,列出在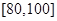 之間的試卷中任取兩份的基本事件,數出基本事件個數,數出至少有一份在
之間的試卷中任取兩份的基本事件,數出基本事件個數,數出至少有一份在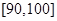 之間的基本事件個數,根據古典概型公式即可求出其概率;(Ⅲ)算出個分數段的頻率,以個分數段的中點值為代表分數乘以相應的概率即平均分數.
之間的基本事件個數,根據古典概型公式即可求出其概率;(Ⅲ)算出個分數段的頻率,以個分數段的中點值為代表分數乘以相應的概率即平均分數.
試題解析:(Ⅰ)分數在 的頻率為
的頻率為 ,由莖葉圖知:分數在
,由莖葉圖知:分數在
之間的頻數為 ,所以全班人數為
,所以全班人數為 , 2分
, 2分
∴分數在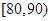 之間的人數
之間的人數
為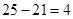 人.則對應的頻率為
人.則對應的頻率為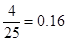 , 3分
, 3分
所以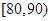 間的矩形的高為
間的矩形的高為 . 4分
. 4分
(Ⅱ)將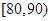 之間的
之間的 個分數編號為
個分數編號為 ,
, 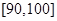 之間的
之間的 個分數
個分數
編號為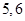 ,在
,在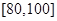 之間的試卷中任取兩份的基本事件為:
之間的試卷中任取兩份的基本事件為: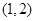 ,
,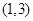 ,
, ,
, ,
,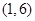 ,
,  ,
, ,
, ,
, ,
, ,
,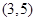 ,
,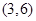 ,
, ,
, ,
,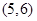 共
共 個. 6分
個. 6分
其中,至少有一份在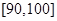 之間的基本事件有
之間的基本事件有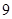 個,故至少有一份分數在
個,故至少有一份分數在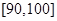 之間的概率是
之間的概率是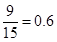 . 8分
. 8分
(Ⅲ)全班人數共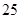 人,根據各分數段人數計算得各分數段的頻率為:
人,根據各分數段人數計算得各分數段的頻率為:分數段


中考特訓營真題分類集訓系列答案
中考先鋒系列答案
中考真題分類卷系列答案
中考智勝考典系列答案
中考總復習導與練系列答案
中考總復習優化方案系列答案
中考最后一套卷系列答案
3年中考2年模擬系列答案
英語聽力模擬試題系列答案
藍皮系列分層強化訓練系列答案
甲品種:271 273 280 285 285 287 292 294 295
301 303 303 307 308 310 314 319 323
325 325 328 331 334 337 352
乙品種:284 292 295 304 306 307 312 313 315
315 316 318 318 320 322 322 324 327
329 331 333 336 337 343 356
由以上數據設計了如下莖葉圖: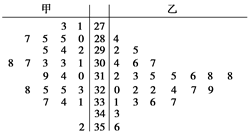
根據以上莖葉圖,對甲、乙兩品種棉花的纖維長度作比較,寫出兩個統計結論:
① ;
② .
(Ⅰ)求甲、乙所選題目分值不同的概率;
(Ⅱ)求甲所選題目分值大于乙所選題目分值的概率.
認為作業多
認為作業不多
合計
喜歡玩手機游戲
18
2
不喜歡玩手機游戲
6
合計
30
(Ⅰ)請將上面的列聯表補充完整(在答題卡上直接填寫結果,不需要寫求解過程);
(Ⅱ)能否在犯錯誤的概率不超過0.005的前提下認為“喜歡玩手機游戲”與“認為作業多”有關系?
(Ⅲ)若從不喜歡玩手機游戲的人中隨機抽取3人,則至少2人認為作業不多的概率是多少?
男生
女生
合計
收看
10
不收看
8
合計
30
已知在這30名同學中隨機抽取1人,抽到“通過電視收看世界杯”的學生的概率是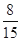 .
.
(I)請將上面的列聯表補充完整,并據此資料分析“通過電視收看世界杯”與性別是否有關?
(II)若從這30名同學中的男同學中隨機抽取2人參加一活動,記“通過電視收看世界杯”的人數為X,求X的分布列和均值.
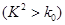
0.100
0.050
0.010
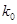
2.706
3.841
6.635
(參考公式: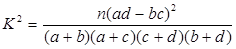 ,
, 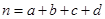 )
)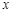
2 3 4 5 6 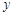
2.2 3.8 5.5 6.5 7.0
若由資料知,y對x呈線性相關關系,試求:
(1)回歸直線方程;
(2)估計使用年限為10年時,維修費用約是多少?
(1) 根據莖葉圖,選手乙的成績中,眾數是多少?選手甲的成績中,中位數是多少?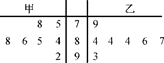
(2) 在流程圖(如圖所示)中,用k表示評委人數,用a表示選手的成績(各評委所給有效分數的平均值).橫線①、②處應填什么?
(3) 根據流程圖,甲、乙的成績分別是多少?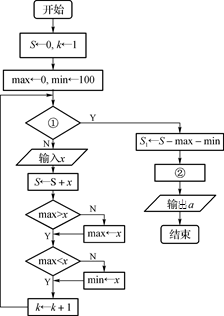


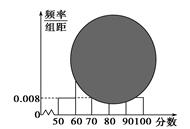
(1)計算頻率分布直方圖中[80,90)間的矩形的高;
(2)若要從分數在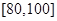 之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份試卷的分數在
之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份試卷的分數在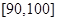 之間的概率;
之間的概率;
(3)根據頻率分布直方圖估計這次測試的平均成績.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號