
 的弧形小路,在路的一側邊緣種植綠化帶.(注:小路及綠化帶的寬度忽略不計)
的弧形小路,在路的一側邊緣種植綠化帶.(注:小路及綠化帶的寬度忽略不計)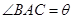 (弧度),將綠化帶總長度表示為
(弧度),將綠化帶總長度表示為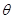 的函數
的函數 ;
;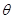 的值,使得綠化帶總長度最大.
的值,使得綠化帶總長度最大.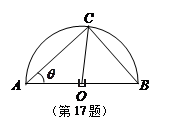
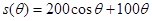 ,
,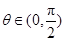 ,(2)當
,(2)當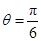 時,綠化帶總長度最大.
時,綠化帶總長度最大. 等于2AC與弧長BC之和. 在直角三角形
等于2AC與弧長BC之和. 在直角三角形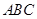 中,
中,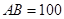 ,
,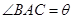 ,所以
,所以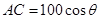 .由于
.由于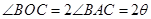 ,所以弧
,所以弧 的長為
的長為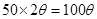 .所以
.所以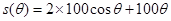 ,作為函數解析式,必須明確其定義域,
,作為函數解析式,必須明確其定義域,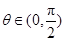 .(2)利用導數求
.(2)利用導數求 最大值. 令
最大值. 令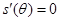 ,則
,則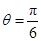 ,列表分析可知當
,列表分析可知當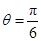 時,
時, 取極大值,即為最大值.
取極大值,即為最大值. ,設圓心為
,設圓心為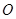 ,連接
,連接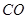 .
.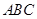 中,
中,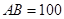 ,
,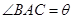 ,
,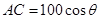 .
.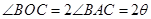 ,所以弧
,所以弧 的長為
的長為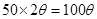 . 3分
. 3分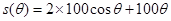 ,
,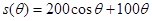 ,
,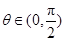 . 7分
. 7分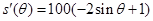 , 9分
, 9分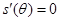 ,則
,則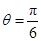 , 11分
, 11分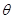 | 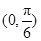 | 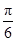 | 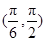 |
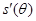 | + | 0 | 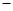 |
 |  | 極大值 |  |
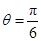 時,
時, 取極大值,即為最大值. 13分
取極大值,即為最大值. 13分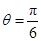 時,綠化帶總長度最大. 14分
時,綠化帶總長度最大. 14分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com