
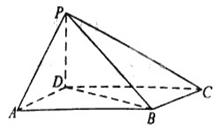
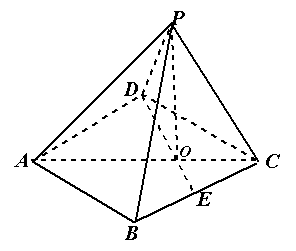
如圖,四棱錐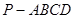 中,底面
中,底面 為平行四邊形,
為平行四邊形,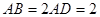 ,
,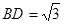 ,
,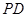 ⊥底面
⊥底面 .
.
(1)證明:平面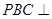 平面
平面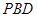 ;
;
(2)若二面角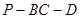 為
為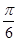 ,求
,求 與平面
與平面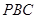 所成角的正弦值.
所成角的正弦值.
(1)證明過程詳見解析;(2)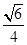 .
.
解析試題分析:(1)可以遵循思路面面垂直 線面垂直
線面垂直 線線垂直,即證明面面垂直只需要證明其中一個面里面的一條直線垂直與另外一個面即可,即證明
線線垂直,即證明面面垂直只需要證明其中一個面里面的一條直線垂直與另外一個面即可,即證明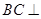 面PDB,線面垂直只需要證明BC與面內(nèi)相交的兩條直線垂直即可,即
面PDB,線面垂直只需要證明BC與面內(nèi)相交的兩條直線垂直即可,即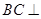 BD,
BD, 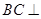 PD,前者可有三角形的勾股定理證得,后者由線面垂直得到
PD,前者可有三角形的勾股定理證得,后者由線面垂直得到
(2)求線面夾角可以利用三維空間直角坐標(biāo)系,分別以DA,DB,PD三條兩兩垂直的直線建立坐標(biāo)系,求面法向量與直線的夾角的余弦值的絕對值即為線面夾角的余弦值.
試題解析:
(1)∵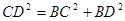 ∴
∴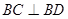
又∵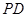 ⊥底面
⊥底面 ∴
∴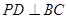
又∵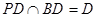 ∴
∴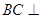 平面
平面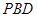
而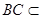 平面
平面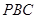 ∴平面
∴平面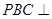 平面
平面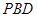 5分
5分
(1)由(1)所證,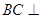 平面
平面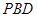 ,所以∠
,所以∠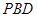 即為二面角P-BC-D的平面角,即∠
即為二面角P-BC-D的平面角,即∠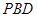
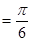
而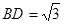 ,所以
,所以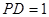 7分
7分
分別以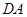 、
、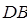 、
、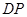 為
為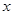 軸、
軸、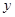 軸、
軸、 軸建立空間直角坐標(biāo)系.則
軸建立空間直角坐標(biāo)系.則 ,
, ,
,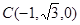 ,
, 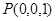 ,所以,
,所以,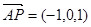 ,
,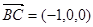 ,
,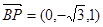 ,設(shè)平面
,設(shè)平面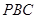 的法向量為
的法向量為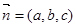 ,則
,則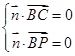 ,即
,即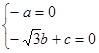 可解得
可解得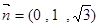 ∴
∴ 與平面
與平面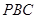 所成角的正弦值為
所成角的正弦值為 12分
12分
考點:面面垂直 線面夾角


 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學(xué)業(yè)水平測試系列答案
浙江之星學(xué)業(yè)水平測試系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,四棱柱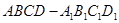 中,
中,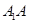
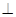 底面
底面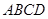 .四邊形
.四邊形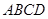 為梯形,
為梯形, ,且
,且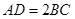 .過
.過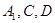 三點的平面記為
三點的平面記為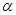 ,
,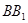 與
與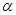 的交點為
的交點為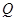 .
.
(1)證明: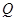 為
為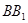 的中點;
的中點;
(2)求此四棱柱被平面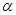 所分成上下兩部分的體積之比;
所分成上下兩部分的體積之比;
(3)若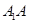
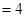 ,
,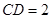 ,梯形
,梯形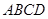 的面積為6,求平面
的面積為6,求平面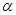 與底面
與底面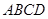 所成二面角大小.
所成二面角大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知四棱錐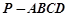 的底面是平行四邊形,
的底面是平行四邊形,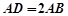 ,
,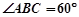 ,
,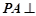 面
面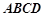 ,
,
且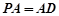 .若
.若 為
為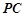 中點,
中點,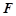 為線段
為線段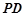 上的點,且
上的點,且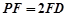 .
.
(1)求證: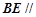 平面
平面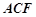 ;
;
(2)求PC與平面PAD所成角的正弦值.
 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,已知四棱錐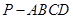 的底面的菱形,
的底面的菱形,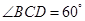 ,點
,點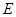 是
是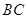 邊的中點,
邊的中點,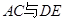 交于點
交于點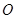 ,
,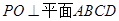
(1)求證: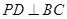 ;
;
(2)若 的大小;
的大小;
(3)在(2)的條件下,求異面直線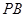 與
與 所成角的余弦值。
所成角的余弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在直角梯形ABCP中,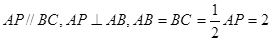 ,D是AP的中點,E,G分別為PC,CB的中點,將三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中點,求證:AP
,D是AP的中點,E,G分別為PC,CB的中點,將三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中點,求證:AP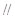 平面EFG;(2)當(dāng)二面角G-EF-D的大小為
平面EFG;(2)當(dāng)二面角G-EF-D的大小為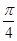 時,求FG與平面PBC所成角的余弦值.
時,求FG與平面PBC所成角的余弦值.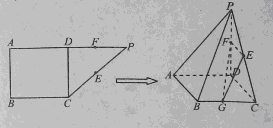
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,已知在四棱錐 中,底面
中,底面 是矩形,
是矩形,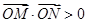 平面
平面 ,
, ,
, ,
, 是
是 的中點,
的中點, 是線段
是線段 上的點.
上的點.
(1)當(dāng) 是
是 的中點時,求證:
的中點時,求證: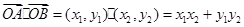 平面
平面 ;
;
(2)要使二面角 的大小為
的大小為 ,試確定
,試確定 點的位置.
點的位置.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖, 已知四邊形ABCD和BCEG均為直角梯形,AD∥BC,CE∥BG,且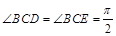 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.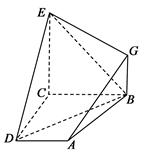
(1)求證:AG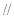 平面BDE;
平面BDE;
(2)求:二面角G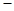 DE
DE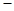 B的余弦值.
B的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,在多面體ABCD-A1B1C1D1中,上、下兩個底面A1B1C1D1和ABCD互相平行,且都是正方形,DD1⊥底面ABCD,AB∥A1B1,AB=2A1B1=2DD1=2a.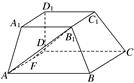
(1)求異面直線AB1與DD1所成角的余弦值;
(2)已知F是AD的中點,求證:FB1⊥平面BCC1B1.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com