
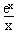 ,
,  ,
,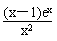 =0得x=1,
=0得x=1,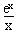 有且只有一解等價于b=e;
有且只有一解等價于b=e;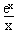 有且只有一解等價于b∈(-∞,0);
有且只有一解等價于b∈(-∞,0);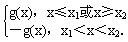 ,
,

 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源:浙江省杭州十四中2011-2012學年高三2月月考試題-數學(理) 題型:解答題
已知函數f (x)=lnx,g(x)=ex.
(I)若函數φ (x) =
f (x)-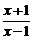 ,求函數φ (x)的單調區間;
,求函數φ (x)的單調區間;
(Ⅱ)設直線l為函數 y=f (x) 的圖象上一點A(x0,f (x0))處的切線.證明:在區間(1,+∞)上存在唯一的x0,使得直線l與曲線y=g(x)相切.
注:e為自然對數的底數.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知函數f(x)=ex+x,g(x)=ln x+x,h(x)=ln x-1的零點依次為a,b,c,則( )
A.a<b<c B.c<b<a C.c<a<b D.b<a<c
查看答案和解析>>
科目:高中數學 來源: 題型:
已知函數f(x)=ex+x,g(x)=ln x+x,h(x)=ln x-1的零點依次為a,b,c,則( )
A.a<b<c B.c<b<a
C.c<a<b D.b<a<c
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com