
(本小題滿分13分)
已知二次函數(shù) ,直線
,直線 ,直線
,直線
 (其中
(其中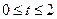 ,
, 為常數(shù));.若直線
為常數(shù));.若直線 1、
1、 2與函數(shù)
2與函數(shù) 的圖象以及
的圖象以及 、
、 軸與函數(shù)
軸與函數(shù) 的圖象所圍成的封閉圖形如圖陰影所示.
的圖象所圍成的封閉圖形如圖陰影所示.
(Ⅰ)求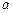 、
、 、
、 的值;
的值;
(Ⅱ)求陰影面積 關(guān)于
關(guān)于 的函數(shù)
的函數(shù) 的解析式;
的解析式;
(Ⅲ)若 問(wèn)是否存在實(shí)數(shù)
問(wèn)是否存在實(shí)數(shù) ,使得
,使得 的圖象與
的圖象與 的圖象有且只有兩個(gè)不同的交點(diǎn)?若存在,求出
的圖象有且只有兩個(gè)不同的交點(diǎn)?若存在,求出 的值;若不存在,說(shuō)明理由.
的值;若不存在,說(shuō)明理由.
解:(I)由圖形可知二次函數(shù)的圖象過(guò)點(diǎn)(0,0),(8,0),并且 的最大值為16
的最大值為16
則 ,
,
∴函數(shù) 的解析式為
的解析式為 ……………4分
……………4分
(Ⅱ)由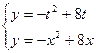 得
得
∵0≤t≤2,∴直線 與
與 的圖象的交點(diǎn)坐標(biāo)為(
的圖象的交點(diǎn)坐標(biāo)為(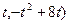 ……………6分
……………6分
由定積分的幾何意義知:
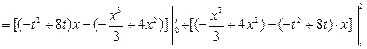
 ……………9分
……………9分
(Ⅲ)令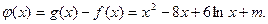
因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/3d/7/lmsmu3.gif" style="vertical-align:middle;" />,要使函數(shù) 與函數(shù)
與函數(shù) 有且僅有2個(gè)不同的交點(diǎn),則函數(shù)
有且僅有2個(gè)不同的交點(diǎn),則函數(shù) 的圖象與
的圖象與 軸的正半軸有且只有兩個(gè)不同的交點(diǎn)
軸的正半軸有且只有兩個(gè)不同的交點(diǎn)
∴ =1或
=1或 =3時(shí),
=3時(shí),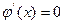
當(dāng) ∈(0,1)時(shí),
∈(0,1)時(shí), 是增函數(shù),當(dāng)
是增函數(shù),當(dāng) ∈(1,3)時(shí),
∈(1,3)時(shí), 是減函數(shù),當(dāng)
是減函數(shù),當(dāng) ∈(3,+∞)時(shí),
∈(3,+∞)時(shí), 是增函數(shù)
是增函數(shù)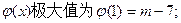
 ……………12分
……………12分
又因?yàn)楫?dāng) →0時(shí),
→0時(shí), ;當(dāng)
;當(dāng)
所以要使 有且僅有兩個(gè)不同的正根,必須且只須
有且僅有兩個(gè)不同的正根,必須且只須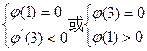
即 ,∴
,∴ 或
或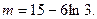
∴當(dāng) 或
或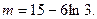 時(shí),函數(shù)
時(shí),函數(shù) 與
與 的圖象有且只有兩個(gè)不同交點(diǎn)。…………14分
的圖象有且只有兩個(gè)不同交點(diǎn)。…………14分
解析


 倍速訓(xùn)練法直通中考考點(diǎn)系列答案
倍速訓(xùn)練法直通中考考點(diǎn)系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業(yè)本系列答案
名校作業(yè)本系列答案 輕巧奪冠周測(cè)月考直通名校系列答案
輕巧奪冠周測(cè)月考直通名校系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)
(1)當(dāng) 時(shí),求函數(shù)
時(shí),求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù) 的圖像在點(diǎn)
的圖像在點(diǎn) 處的切線的傾斜角為
處的切線的傾斜角為 ,問(wèn):
,問(wèn): 在什么范圍取值時(shí),函數(shù)
在什么范圍取值時(shí),函數(shù) 在區(qū)間
在區(qū)間 上總存在極值?
上總存在極值?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某工廠生產(chǎn)某種產(chǎn)品,已知該產(chǎn)品的月生產(chǎn)量 (噸)與每噸產(chǎn)品的價(jià)格p(元/噸)之間的關(guān)系式為:p=24200-0.2x2,且生產(chǎn)x噸的成本為
(噸)與每噸產(chǎn)品的價(jià)格p(元/噸)之間的關(guān)系式為:p=24200-0.2x2,且生產(chǎn)x噸的成本為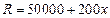 (元).問(wèn)該廠每月生產(chǎn)多少噸產(chǎn)品才能使利潤(rùn)達(dá)到最大?最大利潤(rùn)是多少?(注:利潤(rùn)=收入─成本)
(元).問(wèn)該廠每月生產(chǎn)多少噸產(chǎn)品才能使利潤(rùn)達(dá)到最大?最大利潤(rùn)是多少?(注:利潤(rùn)=收入─成本)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分14分)
已知函數(shù) 在(0,1)內(nèi)是增函數(shù).
在(0,1)內(nèi)是增函數(shù).
(1)求實(shí)數(shù) 的取值范圍;
的取值范圍;
(2)若 ,求證:
,求證: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分13分)已知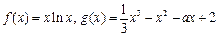 .
.
(1)求函數(shù)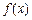 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若對(duì)任意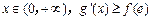 恒成立,求實(shí)數(shù)a的取值范圍.
恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分13分)設(shè)函數(shù)f(x)=x3+ax2-a2x+m(a>0).
(Ⅰ)求函數(shù)f(x)的單調(diào)區(qū)間;
(Ⅱ)若函數(shù)f(x)在x∈[-1,1]內(nèi)沒(méi)有極值點(diǎn),求a的取值范圍;
(Ⅲ)若對(duì)任意的a∈[ 3,6],不等式f(x)≤1在x∈[-2,2]上恒成立,求m的取值范圍.
3,6],不等式f(x)≤1在x∈[-2,2]上恒成立,求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知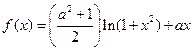

 .
.
(1)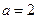 時(shí),求
時(shí),求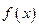 的極值
的極值
(2)當(dāng)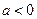 時(shí),討論
時(shí),討論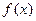 的單調(diào)性。
的單調(diào)性。
(3)證明: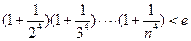 (
(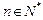 ,
,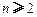 ,其中無(wú)理數(shù)
,其中無(wú)理數(shù)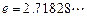 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
.(本小題滿分12分)
已知以函數(shù)f(x)=mx3-x的圖象上一點(diǎn)N(1,n)為切點(diǎn)的切線傾斜角為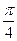 .
.
(1)求m、n的值;
(2)是否存在最小的正整數(shù)k,使得不等式f(x)≤k-1995,對(duì)于x∈[-1,3]恒成立 ?若存在,求出最小的正整數(shù)k,否則請(qǐng)說(shuō)明理由.
?若存在,求出最小的正整數(shù)k,否則請(qǐng)說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com