
已知函數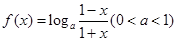 .
.
(1)求函數 的定義域
的定義域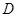 ,并判斷
,并判斷 的奇偶性;
的奇偶性;
(2)用定義證明函數 在
在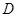 上是增函數;
上是增函數;
(3)如果當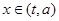 時,函數
時,函數 的值域是
的值域是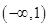 ,求
,求 與
與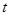 的值.
的值.
.解:(1)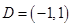 ,函數
,函數 是奇函數.
是奇函數.
(2)設、算、證、結
(3)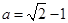 ,
,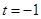
解析試題分析:
思路分析:(1)由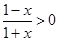 ,求得
,求得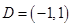
計算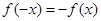 知函數
知函數 是奇函數.
是奇函數.
另證:對任意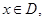
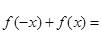 0,
0,
(2)利用“定義”“設、算、證、結”。
(3)根據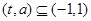 且
且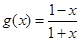 在
在 的值域是
的值域是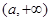 ,
,
得到a的方程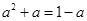 解得
解得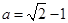 (
(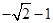 舍去)
舍去)
得到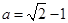 ,
,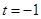 。
。
解:(1)令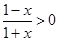 ,解得
,解得 ,
,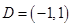
對任意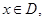
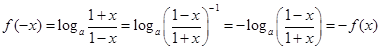
所以函數 是奇函數.
是奇函數.
另證:對任意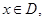
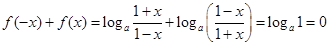 ,
,
所以函數 是奇函數.
是奇函數.
(2)設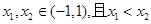 ,
, 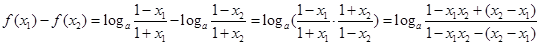
∴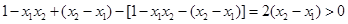
∴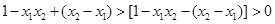
∴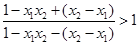 ∵
∵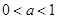 ∴
∴
∴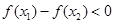 ,∴
,∴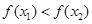
所以函數 在
在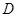 上是增函數.
上是增函數.
(3)由(2)知,函數 在
在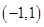 上是增函數,
上是增函數,
又因為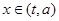 時,
時, 的值域是
的值域是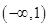 ,
,
所以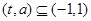 且
且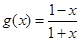 在
在 的值域是
的值域是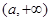 ,
,
故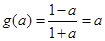 且
且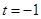 (結合
(結合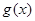 圖像易得
圖像易得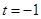 )
)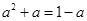 解得
解得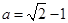 (
(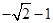 舍去)
舍去)
所以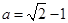 ,
,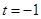
考點:對數函數的性質,函數的奇偶性、單調性。
點評:中檔題,本題主要考查對數函數的性質,利用函數的奇偶性、單調性定義,判斷函數的奇偶性,證明函數的單調性,屬于基礎題目。


科目:高中數學 來源: 題型:解答題
某工廠某種產品的年固定成本為250萬元,每生產 千件,需另投入成本為
千件,需另投入成本為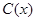 ,當年產量不足80千件時,
,當年產量不足80千件時, (萬元).當年產量不小于80千件時,
(萬元).當年產量不小于80千件時, (萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(Ⅰ)寫出年利潤 (萬元)關于年產量
(萬元)關于年產量 (千件)的函數解析式;
(千件)的函數解析式;
(Ⅱ)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數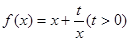 和點
和點 ,過點
,過點 作曲線
作曲線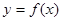 的兩條切線
的兩條切線 、
、 ,切點分別為
,切點分別為 、
、 .
.
(Ⅰ)設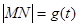 ,試求函數
,試求函數 的表達式;
的表達式;
(Ⅱ)是否存在 ,使得
,使得 、
、 與
與 三點共線.若存在,求出
三點共線.若存在,求出 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(Ⅲ)在(Ⅰ)的條件下,若對任意的正整數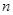 ,在區(qū)間
,在區(qū)間 內總存在
內總存在 個實數
個實數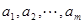 ,
, ,使得不等式
,使得不等式 成立,求
成立,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了降低能源損耗,某城市對新建住宅的屋頂和外墻都要求建造隔熱層.某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元.該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度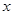 (單位:cm)滿足關系:
(單位:cm)滿足關系: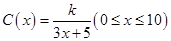 ,若不建隔熱層,每年能源消耗費用為8萬元.設
,若不建隔熱層,每年能源消耗費用為8萬元.設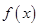 為隔熱層建造費用與20年的能源消耗費用之和.
為隔熱層建造費用與20年的能源消耗費用之和.
(1)求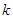 的值及
的值及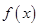 的表達式;
的表達式;
(2)隔熱層修建多厚時,總費用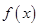 達到最小,并求最小值.
達到最小,并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
隨著機構改革工作的深入進行,各單位要減員增效。有一家公司現有職員 人,(
人,( ,且
,且 為偶數),每人每年可創(chuàng)利
為偶數),每人每年可創(chuàng)利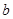 萬元。據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年可多創(chuàng)利
萬元。據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年可多創(chuàng)利 萬元,但公司需支付下崗職員每人每年
萬元,但公司需支付下崗職員每人每年 萬元的生活費,并且該公司正常運轉所需人數不得小于現有員工的
萬元的生活費,并且該公司正常運轉所需人數不得小于現有員工的 ,為獲得最大的經濟效益,該公司應裁員多少人?
,為獲得最大的經濟效益,該公司應裁員多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數f(x)滿足條件f(0)=1和f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在區(qū)間[-1,1]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知冪函數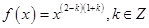 ,且
,且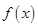 在
在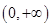 上單調遞增.
上單調遞增.
(1)求實數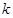 的值,并寫出相應的函數
的值,并寫出相應的函數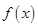 的解析式;
的解析式;
(2)若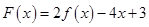 在區(qū)間
在區(qū)間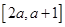 上不單調,求實數
上不單調,求實數 的取值范圍;
的取值范圍;
(3)試判斷是否存在正數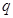 ,使函數
,使函數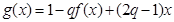 在區(qū)間
在區(qū)間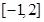 上的值域為
上的值域為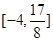 若存在,求出
若存在,求出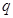 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com