
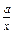 (a>0)的單調性.
(a>0)的單調性. ]、[
]、[ ,+∞)上為增函數;f(x)分別在[-
,+∞)上為增函數;f(x)分別在[- ,0)、(0,
,0)、(0, ]上為減函數
]上為減函數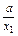 )-(x2+
)-(x2+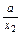 )=(x1-x2)·(1-
)=(x1-x2)·(1-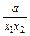 ).
). 時,
時,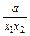 >1,
>1, ]上是減函數.
]上是減函數. 時,0<
時,0<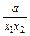 <1,則f(x1)-f(x2)>0,即f(x1)>f(x2),
<1,則f(x1)-f(x2)>0,即f(x1)>f(x2), ,+∞)上是增函數.∵f(x)是奇函數,
,+∞)上是增函數.∵f(x)是奇函數, ]、[
]、[ ,+∞)上為增函數;f(x)分別在[-
,+∞)上為增函數;f(x)分別在[- ,0)、(0,
,0)、(0, ]上為減函數.
]上為減函數.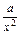 =0可得x=±
=0可得x=±
 時或x<-
時或x<- 時,f ′(x)>0,∴f(x)分別在(
時,f ′(x)>0,∴f(x)分別在( ,+∞)、(-∞,-
,+∞)、(-∞,- ]上是增函數.
]上是增函數. 或-
或- <x<0時,f′(x)<0
<x<0時,f′(x)<0 ]、[-
]、[- ,0)上是減函數.
,0)上是減函數.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com