如圖,MN為兩圓的公共弦,一條直線與兩圓及公共弦依次交于A,B,C,D,E,
求證:AB·CD=BC·DE.
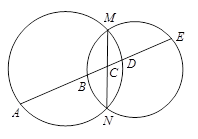
試題分析:由相交弦定理:圓內(nèi)的兩條相交弦,被交點分成的兩條線段長的積相等,得
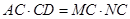
,
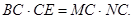
利用等量代換,得到

結(jié)合要證的結(jié)論,將
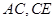
轉(zhuǎn)化為
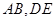
變形即得結(jié)論.
試題解析:證明:由相交弦定理,得
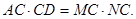
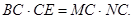
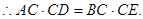
3分
即
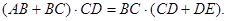
6分
也即
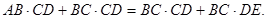
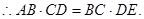
10分
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知圓方程

.
(1)若圓與直線

相交于M,N兩點,且

(

為坐標(biāo)原點)求

的值;
(2)在(1)的條件下,求以

為直徑的圓的方程.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知圓心為C的圓,滿足下列條件:圓心C位于x軸正半軸上,與直線3x-4y+7=0相切,且被
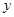
軸截得的弦長為
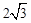
,圓C的面積小于13.
(Ⅰ)求圓C的標(biāo)準(zhǔn)方程;
(Ⅱ)設(shè)過點M(0,3)的直線l與圓C交于不同的兩點A,B,以O(shè)A,OB為鄰邊作平行四邊形OADB.是否存在這樣的直線l,使得直線OD與MC恰好平行?如果存在,求出l的方程;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知點
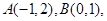
動點P滿足
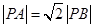
.
(Ⅰ)若點
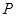
的軌跡為曲線
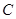
,求此曲線的方程;
(Ⅱ)若點
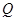
在直線
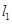
:
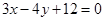
上,直線
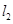
經(jīng)過點
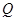
且與曲線
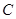
有且只有一個公共點
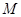
,求
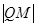
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
以兩點A(-3,-1)和B(5,5)為直徑端點的圓的方程是_________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
如圖,兩個等圓⊙

與⊙

外切,過

作⊙

的兩條切線


是切點,點

在圓

上且不與點

重合,則

=
.

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知圓

與x軸切于A點,與y軸切于B點,設(shè)劣弧

的中點為M,則過點M的圓C的切線方程是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知點

在圓
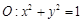
外, 則直線

與圓

的位置關(guān)系是_______.
查看答案和解析>>


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案 .
. 相交于M,N兩點,且
相交于M,N兩點,且 (
( 為坐標(biāo)原點)求
為坐標(biāo)原點)求 的值;
的值; 為直徑的圓的方程.
為直徑的圓的方程. 軸截得的弦長為
軸截得的弦長為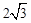 ,圓C的面積小于13.
,圓C的面積小于13.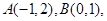 動點P滿足
動點P滿足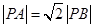 .
.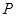 的軌跡為曲線
的軌跡為曲線 ,求此曲線的方程;
,求此曲線的方程;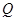 在直線
在直線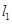 :
: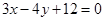 上,直線
上,直線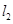 經(jīng)過點
經(jīng)過點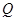 且與曲線
且與曲線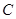 有且只有一個公共點
有且只有一個公共點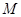 ,求
,求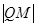 的最小值.
的最小值.