
如圖,三棱錐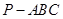 中,
中,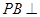 底面
底面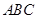 于
于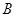 ,
,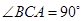 ,
,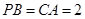 ,點
,點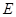 是
是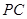 的中點.
的中點.

(1)求證:側面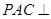 平面
平面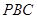 ;
;
(2)若異面直線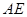 與
與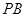 所成的角為
所成的角為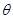 ,且
,且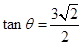 ,
,
求二面角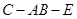 的大小.
的大小.
(1)對于線面垂直的證明,主要是利用判定定理,然后結合這個條件來得到面面垂直的證明。
(2)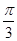
【解析】
試題分析:解:(1)∵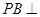 底面
底面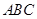 ,
, 平面
平面 ,
,
∴ 平面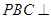 平面
平面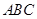 , 又∵
, 又∵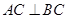 ,
,
平面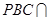 平面
平面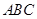
 , ∴
, ∴  平面
平面 3分
3分
而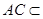 平面
平面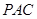 ∴側面
∴側面 平面
平面 .
5分
.
5分
(2)取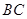 的中點
的中點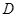 ,則
,則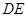 是
是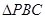 的中位線
的中位線
故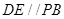 ,所以
,所以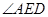 就是異面直線
就是異面直線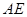 與
與 所成的角
所成的角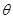 , 7分
, 7分
設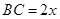 ,則在
,則在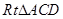 中,
中,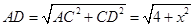 ,
,
在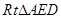 中,
中,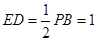 ,∴
,∴ 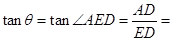
 ,
,
而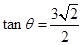 ,∴
,∴  ,即
,即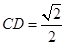 .
9分
.
9分
過 作
作 于點
于點 ,連
,連 . ∵
. ∵
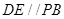 ,
,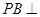 底面
底面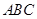
∴ 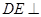 底面
底面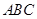 ,從而
,從而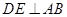 ,又∵
,又∵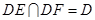 ,
,
∴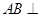 平面
平面 ,從而
,從而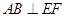 ,
,
所以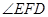 就是二面角
就是二面角 的平面角. 11分
的平面角. 11分
由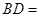
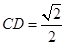 ,得
,得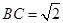 ,
由
,
由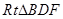 ∽
∽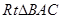 ,
,
可得 ,即
,即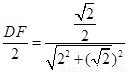 解得
解得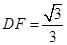 ,
,
在 中,
中, ,所以
,所以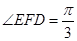 ,
,
故二面角 的大小為
的大小為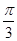 .
14分
.
14分
解法2:如圖,以 為原點,以
為原點,以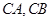 分別為
分別為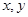 軸建立直角坐標系.
軸建立直角坐標系.

設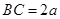 ,則
,則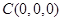 ,
,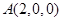 ,
,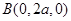 ,
,
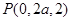 ,從而
,從而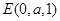 .
.
∴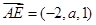 ,
, , 7分
, 7分
∵異面直線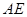 與
與 所成的角為
所成的角為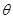 ,且
,且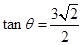 ,
,
∴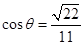 ,
,
又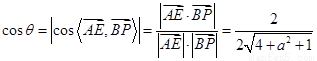 ,
,
從而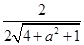
 ,解得
,解得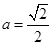 ...
9分
...
9分
∴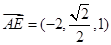 ,
,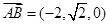 ,
, ,
,
設平面 的法向量為
的法向量為 ,則由
,則由
得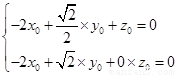 , 令
, 令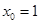 ,得
,得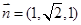 .
11分
.
11分
又平面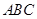 的法向量為
的法向量為 , 12分
, 12分
∴
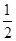 ,∴
,∴  ,
,
所以二面角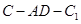 的大小為
的大小為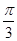 .
14分
.
14分
考點:面面垂直,二面角
點評:主要是考查了空間幾何體中垂直的證明以及異面直線的角和二面角的平面角的借助于向量來求解,屬于中檔題。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
如圖:三棱錐![]() 中,
中,![]() ^底面
^底面![]() ,若底面
,若底面![]() 是邊長為2的正三角形,且
是邊長為2的正三角形,且![]() 與底面
與底面![]() 所成的角為
所成的角為![]() .若
.若![]() 是
是![]() 的中點,求:
的中點,求:
(1)三棱錐![]() 的體積;
的體積;
|

(2)異面直線![]() 與
與![]() 所成角的大小(結果用反三角函數值表示).
所成角的大小(結果用反三角函數值表示).
查看答案和解析>>
科目:高中數學 來源:2014屆浙江省溫州八校高三9月期初聯考理科數學試卷(解析版) 題型:解答題
如圖,三棱錐 中,
中, 底面
底面 ,
, ,
, ,
, 為
為 的中點,點
的中點,點 在
在 上,且
上,且 .
.

(Ⅰ)求證:平面 平面
平面 ;
;
(Ⅱ)求平面 與平面
與平面 所成的二面角的平面角(銳角)的余弦值.
所成的二面角的平面角(銳角)的余弦值.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市青浦區高三上學期期終學習質量調研測試數學試卷 題型:解答題
(本題滿分12分) 本題共有2個小題,第1小題滿分6分,第2小題滿分6分.
如圖:三棱錐 中,
中, ^底面
^底面 ,若底面
,若底面 是邊長為2的正三角形,且
是邊長為2的正三角形,且
與底面 所成的角為
所成的角為 ,若
,若 是
是 的中點,
的中點,
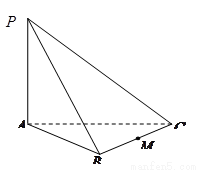
求:(1)三棱錐 的體積;
的體積;
(2)異面直線 與
與 所成角的大小(結果用反三角函數值表示).
所成角的大小(結果用反三角函數值表示).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com