
已知函數(shù) .
.
(1) 當(dāng) 時,求函數(shù)
時,求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2) 當(dāng) 時,函數(shù)
時,函數(shù) 圖象上的點都在
圖象上的點都在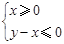 所表示的平面區(qū)域內(nèi),求實數(shù)
所表示的平面區(qū)域內(nèi),求實數(shù)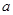 的取值范圍.
的取值范圍.
(1) 函數(shù) 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為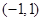 ,單調(diào)遞減區(qū)間為
,單調(diào)遞減區(qū)間為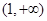 ;(2)
;(2)  .
.
解析試題分析:本小題主要通過函數(shù)與導(dǎo)數(shù)綜合應(yīng)用問題,具體涉及到用導(dǎo)數(shù)來研究函數(shù)的單調(diào)性等知識內(nèi)容,考查考生的運算求解能力,推理論證能力,其中重點對導(dǎo)數(shù)對函數(shù)的描述進(jìn)行考查,本題是一道難度較高且綜合性較強(qiáng)的壓軸題,也是一道關(guān)于數(shù)列拆分問題的典型例題,對今后此類問題的求解有很好的導(dǎo)向作用.(1)代入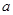 的值,明確函數(shù)解析式,并注明函數(shù)的定義域,然后利用求導(dǎo)研究函數(shù)的單調(diào)性;(2)利用構(gòu)造函數(shù)思想,構(gòu)造
的值,明確函數(shù)解析式,并注明函數(shù)的定義域,然后利用求導(dǎo)研究函數(shù)的單調(diào)性;(2)利用構(gòu)造函數(shù)思想,構(gòu)造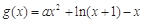 ,然后利用轉(zhuǎn)化思想,將問題轉(zhuǎn)化為只需
,然后利用轉(zhuǎn)化思想,將問題轉(zhuǎn)化為只需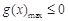 ,下面通過對
,下面通過對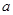 進(jìn)行分類討論進(jìn)行研究函數(shù)的單調(diào)性,明確最值進(jìn)而確定
進(jìn)行分類討論進(jìn)行研究函數(shù)的單調(diào)性,明確最值進(jìn)而確定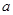 的取值范圍.
的取值范圍.
試題解析:(1) 當(dāng)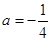 時,
時,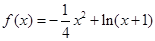
 ,
,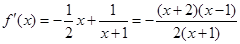
 ,
,
由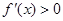 解得
解得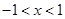 ,由
,由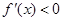 解得
解得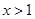 .
.
故函數(shù) 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為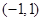 ,單調(diào)遞減區(qū)間為
,單調(diào)遞減區(qū)間為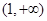 . (6分)
. (6分)
(2) 因函數(shù)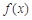 圖象上的點都在
圖象上的點都在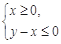 所表示的平面區(qū)域內(nèi),
所表示的平面區(qū)域內(nèi),
則當(dāng)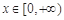 時,不等式
時,不等式 恒成立,即
恒成立,即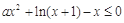 恒成立,、
恒成立,、
設(shè)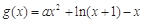 (
(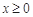 ),只需
),只需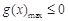 即可.
即可.
由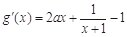
 ,
,
(i) 當(dāng)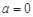 時,
時,  ,
,
當(dāng)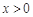 時,
時,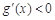 ,函數(shù)
,函數(shù)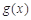 在
在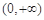 上單調(diào)遞減,故
上單調(diào)遞減,故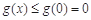 成立.
成立.
(ii) 當(dāng) 時,由
時,由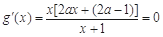 ,因
,因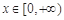 ,所以
,所以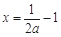 ,
,
① 若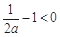 ,即
,即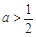 時,在區(qū)間
時,在區(qū)間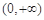 上,
上,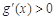 ,
,
則函數(shù)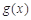 在
在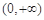 上單調(diào)遞增,
上單調(diào)遞增,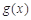 在
在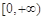 上無最大值,當(dāng)
上無最大值,當(dāng)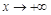 時,
時, 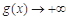 ,此時不滿足條件;
,此時不滿足條件;
② 若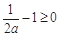 ,即
,即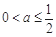 時,函數(shù)
時,函數(shù)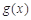 在
在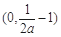 上單調(diào)遞減,
上單調(diào)遞減,
在區(qū)間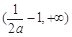 上單調(diào)遞增,同樣
上單調(diào)遞增,同樣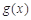 在
在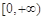 上無最大值,當(dāng)
上無最大值,當(dāng)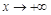 時,
時, 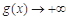 ,不滿足條件.
,不滿足條件.
(iii) 當(dāng)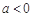 時,由
時,由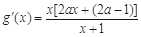 ,∵
,∵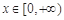 ,∴
,∴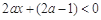 ,
,
∴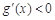 ,故函數(shù)
,故函數(shù)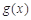 在
在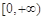 上單調(diào)遞減,故
上單調(diào)遞減,故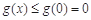 成立.
成立.
綜上所述,實數(shù)a的取值范圍是 . (12分)
. (12分)
考點:(1)函數(shù)的單調(diào)區(qū)間;(2)導(dǎo)數(shù)的應(yīng)用.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)m為實數(shù),函數(shù)f(x)=-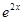 +2x+m,x∈R
+2x+m,x∈R
(Ⅰ)求f(x)的單調(diào)區(qū)間與極值;
(Ⅱ)求證:當(dāng)m≤1且x>0時,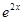 >2
>2 +2mx+1.
+2mx+1.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
 .
.
(Ⅰ)若 在
在 處的切線垂直于直線
處的切線垂直于直線 ,求該點的切線方程,并求此時函數(shù)
,求該點的切線方程,并求此時函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若 對任意的
對任意的 恒成立,求實數(shù)
恒成立,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知 為函數(shù)
為函數(shù) 圖象上一點,O為坐標(biāo)原點,記直線
圖象上一點,O為坐標(biāo)原點,記直線 的斜率
的斜率 .
.
(1)若函數(shù) 在區(qū)間
在區(qū)間
 上存在極值,求實數(shù)m的取值范圍;
上存在極值,求實數(shù)m的取值范圍;
(2)當(dāng)  時,不等式
時,不等式 恒成立,求實數(shù)
恒成立,求實數(shù) 的取值范圍;
的取值范圍;
(3)求證: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知 的導(dǎo)函數(shù)
的導(dǎo)函數(shù) ,且
,且 ,設(shè)
,設(shè) ,
,
且 .
.
(Ⅰ)討論 在區(qū)間
在區(qū)間 上的單調(diào)性;
上的單調(diào)性;
(Ⅱ)求證: ;
;
(Ⅲ)求證: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如下圖,過曲線 :
: 上一點
上一點 作曲線
作曲線 的切線
的切線 交
交 軸于點
軸于點 ,又過
,又過 作
作  軸的垂線交曲線
軸的垂線交曲線 于點
于點 ,然后再過
,然后再過 作曲線
作曲線 的切線
的切線 交
交 軸于點
軸于點 ,又過
,又過 作
作 軸的垂線交曲線
軸的垂線交曲線 于點
于點 ,
, ,以此類推,過點
,以此類推,過點 的切線
的切線 與
與 軸相交于點
軸相交于點 ,再過點
,再過點 作
作 軸的垂線交曲線
軸的垂線交曲線 于點
于點 (
( N
N ).
).
(1) 求 、
、 及數(shù)列
及數(shù)列 的通項公式;(2) 設(shè)曲線
的通項公式;(2) 設(shè)曲線 與切線
與切線 及直線
及直線 所圍成的圖形面積為
所圍成的圖形面積為 ,求
,求 的表達(dá)式; (3) 在滿足(2)的條件下, 若數(shù)列
的表達(dá)式; (3) 在滿足(2)的條件下, 若數(shù)列 的前
的前 項和為
項和為 ,求證:
,求證:
 N
N .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) .
.
(I)若a=-1,求函數(shù)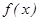 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若函數(shù) 的圖象在點(2,f(2))處的切線的傾斜角為45o,對于任意的t
的圖象在點(2,f(2))處的切線的傾斜角為45o,對于任意的t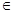 [1,2],函數(shù)
[1,2],函數(shù)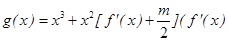 是
是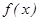 的導(dǎo)函數(shù))在區(qū)間(t,3)上總不是單調(diào)函數(shù),求m的取值范圍;
的導(dǎo)函數(shù))在區(qū)間(t,3)上總不是單調(diào)函數(shù),求m的取值范圍;
(Ⅲ)求證: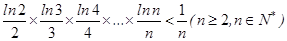
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com