
如圖,在平面直角坐標系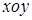 中,
中,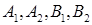 為橢圓
為橢圓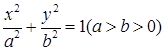 的
的
四個頂點,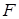 為其右焦點,直線
為其右焦點,直線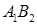 與直線
與直線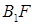 相交于點T,線段
相交于點T,線段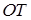 與橢圓的交點
與橢圓的交點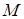 恰為線段
恰為線段 的中點,則該橢圓的離心率為__________.
的中點,則該橢圓的離心率為__________.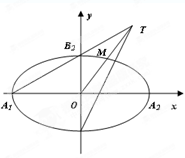
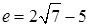
解析試題分析:對橢圓進行壓縮變換,x′=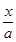 ,y′=
,y′=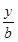 橢圓變為單位圓:x'2+y'2=1,F'(
橢圓變為單位圓:x'2+y'2=1,F'(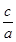 ,0)
,0)
延長TO交圓O于N,易知直線A1B1斜率為1,TM=MO=ON=1,A1B2=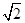 ,
,
設T(x′,y′),則TB2=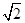 x′,y′=x′+1,由割線定理:TB2×TA1=TM×TN,
x′,y′=x′+1,由割線定理:TB2×TA1=TM×TN, 易知:B1(0,-1)直線B1T方程:
易知:B1(0,-1)直線B1T方程: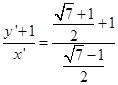 令y′=0,x′=2
令y′=0,x′=2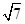 -5,即F橫坐標,即原橢圓的離心率e=2
-5,即F橫坐標,即原橢圓的離心率e=2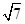 -5
-5
故答案:2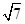 -5。
-5。
考點:本題主要考查了圓錐曲線的性質和應用,解題時要認真審題,仔細解答.
點評:解決該試題的關鍵是對橢圓進行壓縮變換,x′=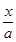 ,y′=
,y′=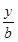 ,橢圓變為單位圓:x'2+y'2=1,F'(
,橢圓變為單位圓:x'2+y'2=1,F'(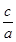 ,0).根據題設條件求出直線B1T方程,直線直線B1T與x軸交點的橫坐標就是該橢圓的離心率.
,0).根據題設條件求出直線B1T方程,直線直線B1T與x軸交點的橫坐標就是該橢圓的離心率.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com