
已知等比數列 的前
的前 項和為
項和為 ,正數數列
,正數數列 的首項為
的首項為 ,
,
且滿足: .記數列
.記數列 前
前 項和為
項和為 .
.
(Ⅰ)求 的值; (Ⅱ)求數列
的值; (Ⅱ)求數列 的通項公式;
的通項公式;
(Ⅲ)是否存在正整數 ,且
,且 ,使得
,使得 成等比數列?若存在,求出
成等比數列?若存在,求出 的值,若不存在,說明理由.
的值,若不存在,說明理由.
(Ⅰ)
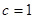 (Ⅱ)
(Ⅱ) 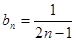
 (Ⅲ) 存在,
(Ⅲ) 存在, 。
。
【解析】熟練掌握并靈活運用等差等比數列的通項公式以及求和公式是解決此題的關鍵.
(Ⅰ)根據Sn求出a1,a2,a3,根據{an}為等比數列,確定出c的值.
(Ⅱ)根據bn+1=
|
bn |
|
1+2bn |
(n∈N*),得到bn與bn+1的遞推關系,根據特殊的數列求通項.
(Ⅲ)先求出Tn,假設滿足T1,Tm,Tn成等比數列,得到n與m的關系式,再根據1<m<n,求出m,n的范圍,根據m,n是正整數,求出m,n的值.
解:(Ⅰ)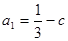 ,
, ,
, ………(3分)
………(3分)
因為 為等比數列所以
為等比數列所以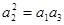 ,得
,得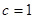 ………………………(4分)
………………………(4分)
經檢驗此時 為等比數列. ………………(5分)
為等比數列. ………………(5分)
(Ⅱ)∵ 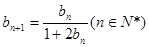 ∴
∴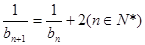
數列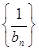 為等差數列 …………………………………………(7分)
為等差數列 …………………………………………(7分)
又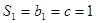 ,所以
,所以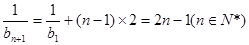
所以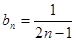
 …………(10分)
…………(10分)
(Ⅲ) ……(12分)
……(12分)
假設存在正整數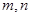 ,且
,且 ,使得
,使得 成等比數列
成等比數列
則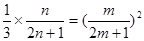 ,所以
,所以
由 得
得 且
且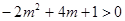
即 ,所以
,所以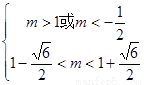
因為 為正整數,所以
為正整數,所以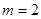 ,此時
,此時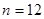
所以滿足題意的正整數存在, .…………(15分)
.…………(15分)


科目:高中數學 來源:2011屆陜西省師大附中、西工大附中高三第七次聯考文數 題型:解答題
(本題13分)
已知等比數列 的前
的前 項和是
項和是 ,滿足
,滿足 .
.
(Ⅰ)求數列 的通項
的通項 及前
及前 項和
項和 ;
;
(Ⅱ)若 數列
數列 滿足
滿足 ,求數列
,求數列 的前
的前 項和
項和 ;
;
(Ⅲ)若對任意的 ,恒有
,恒有 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年吉林省長春市畢業班第四次調研測試文科數學試卷(解析版) 題型:選擇題
已知等比數列 的前
的前 項和為
項和為 ,且滿足
,且滿足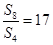 ,則公比
,則公比 =(
)
=(
)
A. B.
B.  C. 2
D.
C. 2
D. 
查看答案和解析>>
科目:高中數學 來源:2013屆廣東省度高二下學期期中文科數學試卷(解析版) 題型:選擇題
已知等比數列{ }的前
}的前 項和為
項和為 ,且
,且 ,則數列
,則數列 的公比
的公比 的值為( )
的值為( )
A. 2 B. 3 C. 2或-3 D. 2或3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com