設函數(shù)
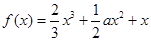
,

∈R
(1)當
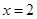
時,
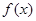
取得極值,求

的值;
(2)若
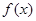
在
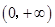
內為增函數(shù),求

的取值范圍.
(1)-
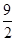
;(2)
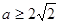
第一問中,利用函數(shù)在給定點處取得極值,說明了該點的導數(shù)值為零。解得參數(shù)a的取值。第二問中,
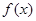
在
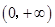
內為增函數(shù)等價于
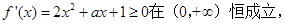
利用分離參數(shù)的思想可以求解得到
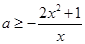
,然后求解右邊函數(shù)的最大值即可。
解:因為

故得到(1)

(2)
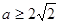
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)f(x)=ex+ax2-ex,a∈R[
(Ⅰ)若曲線y=f(x)在點(1,f(1))處的切線平行于x軸,求函數(shù)f(x)的單調區(qū)間;
(Ⅱ)試確定a的取值范圍,使得曲線y=f(x)上存在唯一的點P,曲線在該點處的切線與曲線只有一個公共點P
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
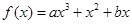
(其中常數(shù)a,b∈R)。
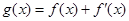
是奇函數(shù).
(Ⅰ)求
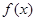
的表達式;
(Ⅱ)求
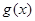
在區(qū)間[1,2]上的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
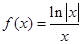
(I)求函數(shù)
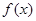
的單調區(qū)間; (II)若關于
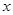
的不等式
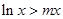
對一切
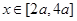
都成立
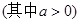
,求實數(shù)
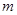
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設函數(shù)
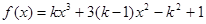
在區(qū)間(0,4)上是減函數(shù),則
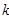
的取值范圍是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)
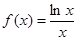
,若方程
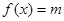
存在兩個不同的實數(shù)解,則實數(shù)
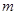
的取值范圍為( ▲ )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若函數(shù)
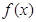
的導數(shù)是
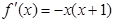
,則函數(shù)
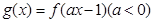
的單調減區(qū)間是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知定義在正實數(shù)集上的函數(shù)
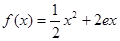
,
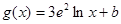
(其中
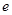
為常數(shù),
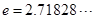
),若這兩個函數(shù)的圖象有公共點,且在該點處的切線相同。
(Ⅰ)求實數(shù)
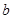
的值;
(Ⅱ)當
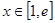
時,
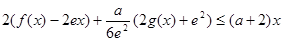
恒成立,求實數(shù)
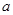
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)

在

上為減函數(shù),則

的取值范圍是
.
查看答案和解析>>

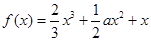 ,
, ∈R
∈R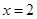 時,
時,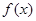 取得極值,求
取得極值,求 的值;
的值;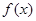 在
在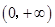 內為增函數(shù),求
內為增函數(shù),求 的取值范圍.
的取值范圍. 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案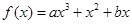 (其中常數(shù)a,b∈R)。
(其中常數(shù)a,b∈R)。 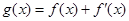 是奇函數(shù).
是奇函數(shù).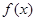 的表達式;
的表達式;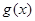 在區(qū)間[1,2]上的最大值和最小值.
在區(qū)間[1,2]上的最大值和最小值.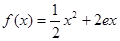 ,
,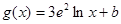 (其中
(其中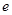 為常數(shù),
為常數(shù),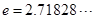 ),若這兩個函數(shù)的圖象有公共點,且在該點處的切線相同。
),若這兩個函數(shù)的圖象有公共點,且在該點處的切線相同。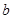 的值;
的值;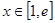 時,
時, 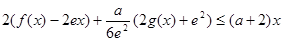 恒成立,求實數(shù)
恒成立,求實數(shù)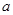 的取值范圍.
的取值范圍.