
已知函數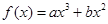 在點
在點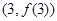 處的切線方程為
處的切線方程為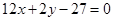 ,且對任意的
,且對任意的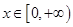 ,
,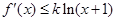 恒成立.
恒成立.
(Ⅰ)求函數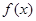 的解析式;
的解析式;
(Ⅱ)求實數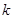 的最小值;
的最小值;
(Ⅲ)求證: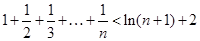 (
(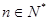 ).
).
(Ⅰ) (Ⅱ)
(Ⅱ)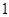
(Ⅲ)先證 ,累加即得.
,累加即得.
【解析】
試題分析:(Ⅰ)將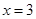 代入直線方程得
代入直線方程得 ,∴
,∴ ①
①
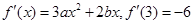 ,∴
,∴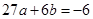 ②
②
聯立,解得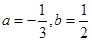 ∴
∴
(Ⅱ) ,∴
,∴ 在
在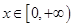 上恒成立;
上恒成立;
即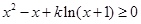 在
在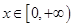 恒成立;
恒成立;
設 ,
, ,
,
∴只需證對于任意的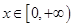 有
有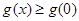
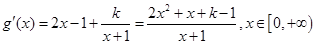
設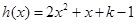 ,
,
1)當 ,即
,即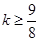 時,
時,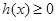 ,∴
,∴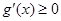
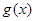 在
在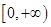 單調遞增,∴
單調遞增,∴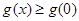
2)當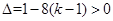 ,即
,即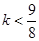 時,設
時,設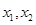 是方程
是方程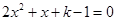 的兩根且
的兩根且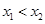
由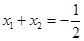 ,可知
,可知 ,分析題意可知當
,分析題意可知當 時對任意
時對任意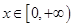 有
有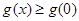 ;
;
∴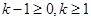 ,∴
,∴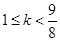
綜上分析,實數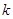 的最小值為
的最小值為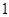 .
.
(Ⅲ)令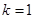 ,有
,有 即
即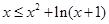 在
在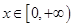 恒成立;
恒成立;
令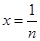 ,得
,得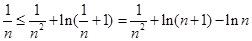
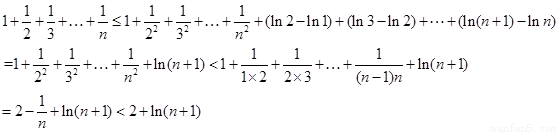
∴原不等式得證.
考點:利用導數研究曲線上某點切線方程;函數解析式的求解及常用方法;不等式的證明.
點評:本題考查了利用導數研究函數的切線方程問題,在曲線上某點處的切線的斜率就是該點的導數值,考查了導數在最大值和最小值中的應用,體現了數學轉化思想和分類討論的數學思想.特別是(Ⅲ)的證明,用到了放縮法和裂項相消,此題屬難度較大的題目.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源:2014屆遼寧省五校協作體屆高三摸底考試理科數學試卷(解析版) 題型:解答題
已知函數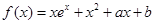 在點
在點 處的切線方程是x+ y-l=0,其中e為自然對數的底數,函數g(x)=1nx- cx+ 1+ c(c>0),對一切x∈(0,+
處的切線方程是x+ y-l=0,其中e為自然對數的底數,函數g(x)=1nx- cx+ 1+ c(c>0),對一切x∈(0,+ )均有
)均有 恒成立.
恒成立.
(Ⅰ)求a,b,c的值;
(Ⅱ)求證: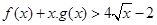 .
.
查看答案和解析>>
科目:高中數學 來源:2014屆云南省高二下學期期末考試文科數學試卷(解析版) 題型:解答題
已知函數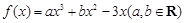 在點
在點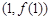 處的切線方程為
處的切線方程為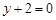 .
.
(1)求函數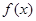 的解析式;
的解析式;
(2)若經過點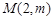 可以作出曲線
可以作出曲線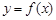 的三條切線,求實數
的三條切線,求實數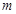 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014屆江西省南昌市高二2月份月考文科數學試卷(解析版) 題型:解答題
(本小題13分)已知函數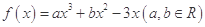 在點
在點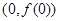 處的切線與直線
處的切線與直線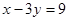 垂直.
垂直.
(1)若對于區間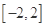 上任意兩個自變量的值
上任意兩個自變量的值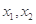 都有
都有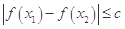 ,求實數
,求實數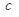 的最小值;
的最小值;
(2)若過點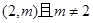 可作曲線
可作曲線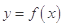 的三條切線,求實數
的三條切線,求實數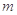 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省蘇南四校高三12月月考試數學試卷(解析版) 題型:解答題
已知函數 在點
在點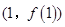 處的切線方程為
處的切線方程為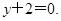
(1)求函數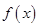 的解析式;
的解析式;
(2)若對于區間[-2,2]上任意兩個自變量的值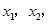 都有
都有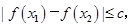 求實數c的最小值.
求實數c的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com