
如圖所示,已知橢圓方程為 ,A為橢圓的左頂點,B、C在橢圓上,若四邊形OABC為平行四邊形,且
,A為橢圓的左頂點,B、C在橢圓上,若四邊形OABC為平行四邊形,且 ,則橢圓的離心率等于( )
,則橢圓的離心率等于( )
A、 B、
B、 C、
C、 D、
D、
C
解析試題分析:令橢圓的右端點為M,連接CM,由題意四邊形OABC為平行四邊形,且∠OAB=45°,B,C在橢圓上,可得∠COM=∠CMO=∠OAB=45°,則有∠OCM=90°,故可得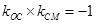 ,又四邊形OABC為平行四邊形,B,C在橢圓上,由圖形知|BC|=a,且BC∥OA由橢圓的對稱性知,B,C兩點關于y軸對稱,故C的橫坐標為
,又四邊形OABC為平行四邊形,B,C在橢圓上,由圖形知|BC|=a,且BC∥OA由橢圓的對稱性知,B,C兩點關于y軸對稱,故C的橫坐標為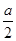 ,代入橢圓的方程得
,代入橢圓的方程得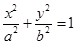 得y=±
得y=±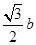 ,由圖形知C(
,由圖形知C(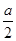 ,
,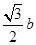 ),故有
),故有 ,∴
,∴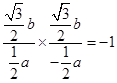 ,解得
,解得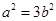 ,故
,故 ,所以
,所以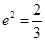
,得e=
考點:本題考查橢圓的簡單性質。
點評:求解本題的關鍵是根據橢圓的對稱性得出點C的坐標以及圖形中的垂直關系,求出點C的坐標是為了表示出斜率,求出垂直關系是為了利用斜率的乘積為-1建立方程,然后再根據求離心率的公式求出離心率即可.本題比較抽象,方法單一,入手較難,運算量不大.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com