
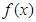 的導數
的導數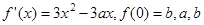 為實數,
為實數,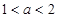 .
.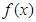 在區間[-1,1]上的最小值、最大值分別為-2、1,求a、b的值;
在區間[-1,1]上的最小值、最大值分別為-2、1,求a、b的值;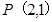 且與曲線
且與曲線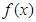 相切的直線
相切的直線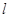 的方程;
的方程;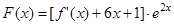 ,試判斷函數
,試判斷函數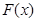 的極值點個數。
的極值點個數。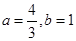 (Ⅱ)
(Ⅱ)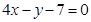 或
或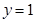 (Ⅲ)
(Ⅲ)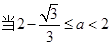 時極值點個數0,當
時極值點個數0,當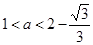 時兩個極值點
時兩個極值點 , 1分
, 1分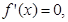 得
得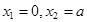 .
.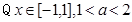 ,當
,當 時,
時,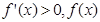 遞增;
遞增;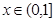 時,
時, ,
,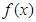 遞減.
遞減.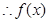 在區間[-1,1]上的最大值為
在區間[-1,1]上的最大值為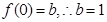 . 2分
. 2分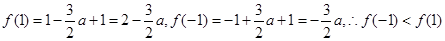 .
.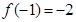 ,即
,即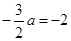 ,得
,得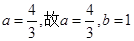 為所求。 4分
為所求。 4分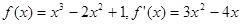 ,點P(2,1)在曲線
,點P(2,1)在曲線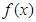 上。
上。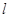 的斜率
的斜率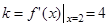 ,
,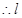 的方程為
的方程為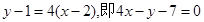 . 5分
. 5分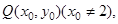 切線
切線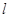 的余率
的余率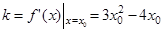 ,
,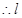 的方程為
的方程為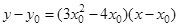 。又點P(2,1)在
。又點P(2,1)在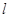 上,
上,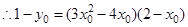 ,
,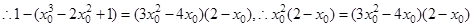 ,
,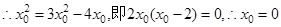 .
. 切線
切線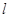 的方程為
的方程為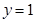 .
.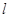 的方程為
的方程為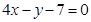 或
或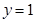 . 8分
. 8分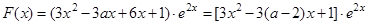 .
.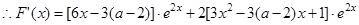 .
.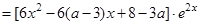 .
. 的判別式為
的判別式為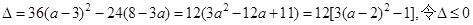 得:
得: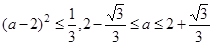 .令
.令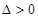 ,得
,得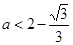 ,或
,或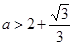 。 10分
。 10分 ,
,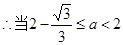 時,
時,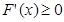 ,函數
,函數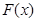 為單調遞增,極值點個數0; 11分
為單調遞增,極值點個數0; 11分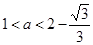 時,此時方程
時,此時方程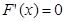 有兩個不相等的實數根,根據極值點的定義,
有兩個不相等的實數根,根據極值點的定義,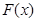 有兩個極值點. 12分
有兩個極值點. 12分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com