
在△ABC中,∠A,∠B,∠C所對(duì)的邊分別是a、b、c,不等式 ≥0對(duì)一切實(shí)數(shù)
≥0對(duì)一切實(shí)數(shù) 恒成立.
恒成立.
(1)求cosC的取值范圍;
(2)當(dāng)∠C取最大值,且△ABC的周長(zhǎng)為6時(shí),求△ABC面積的最大值,并指出面積取最大值時(shí)△ABC的形狀.
(1)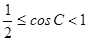 ;(2)
;(2)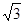 。
。
解析試題分析:(1) 需對(duì) 分情況討論,cosC≠0時(shí),則為一元二次不等式恒成立問(wèn)題,則需
分情況討論,cosC≠0時(shí),則為一元二次不等式恒成立問(wèn)題,則需 ;
;
(2)因?yàn)镾△ABC=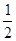
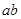
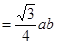 ,只需求
,只需求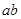 的最大值,再由余弦定理的應(yīng)用及基本不等式去求。
的最大值,再由余弦定理的應(yīng)用及基本不等式去求。
(1)當(dāng)cosC=0時(shí),sinC=1,原不等式即為4x+6≥0對(duì)一切實(shí)數(shù)x不恒成立.
當(dāng)cosC≠0時(shí),應(yīng)有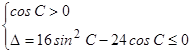
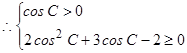 ,解得
,解得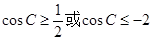 (舍去)
(舍去)
∵C是△ABC的內(nèi)角, ∴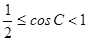
(2)∵0<C<π,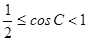
∴∠C的最大值為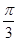 , 此時(shí)
, 此時(shí)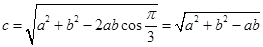 ,
,
∴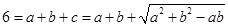 ≥
≥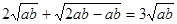 ,
,
∴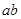 ≤4(當(dāng)且僅當(dāng)a=b時(shí)取“=”),
≤4(當(dāng)且僅當(dāng)a=b時(shí)取“=”),
∴S△ABC=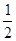
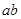
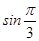 ≤
≤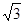 (當(dāng)且僅當(dāng)a=b時(shí)取“=”),
(當(dāng)且僅當(dāng)a=b時(shí)取“=”),
此時(shí),△ABC面積的最大值為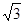 ,△ABC為等邊三角形。
,△ABC為等邊三角形。
考點(diǎn):(1)一元二次不等式的解法;(2)余弦定理的應(yīng)用;(3)利用基本不等式求最值。


 激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)f(x)=msinx+ cosx(m>0)的最大值為2.
cosx(m>0)的最大值為2.
(1)求函數(shù)f(x)在[0,π]上的單調(diào)遞減區(qū)間;(2)△ABC中, 角A,B,C所對(duì)的邊分別是a,b,c, 且C=60°,c=3,求△ABC的面積.
角A,B,C所對(duì)的邊分別是a,b,c, 且C=60°,c=3,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知 三個(gè)內(nèi)角
三個(gè)內(nèi)角 ,
, ,
, 的對(duì)邊分別為
的對(duì)邊分別為 ,
,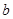 ,
,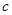 ,且
,且 ,
,
(1)求角
(2)若 =
= ,
, 的面積為
的面積為 ,求
,求 的周長(zhǎng).
的周長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知向量 ,函數(shù)
,函數(shù) .
.
(1)求函數(shù) 的對(duì)稱中心;
的對(duì)稱中心;
(2)在 中,
中, 分別是角
分別是角 對(duì)邊,且
對(duì)邊,且 ,且
,且 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
△ABC的內(nèi)角A,B,C的對(duì)邊分別是a,b,c,已知3acosC=2ccosA,tanA=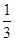 ,求B.
,求B.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖所示,在四邊形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形.
(1)將四邊形ABCD的面積S表示為θ的函數(shù);
(2)求S的最大值及此時(shí)θ角的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖, 、
、 是兩個(gè)小區(qū)所在地,
是兩個(gè)小區(qū)所在地, 、
、 到一條公路
到一條公路 的垂直距離分別為
的垂直距離分別為
 ,
,
 ,
, 兩端之間的距離為
兩端之間的距離為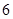
 .
.
(1)某移動(dòng)公司將在 之間找一點(diǎn)
之間找一點(diǎn) ,在
,在 處建造一個(gè)信號(hào)塔,使得
處建造一個(gè)信號(hào)塔,使得 對(duì)
對(duì) 、
、 的張角與
的張角與 對(duì)
對(duì) 、
、 的張角相等,試確定點(diǎn)
的張角相等,試確定點(diǎn) 的位置.
的位置.
(2)環(huán)保部門將在 之間找一點(diǎn)
之間找一點(diǎn) ,在
,在 處建造一個(gè)垃圾處理廠,使得
處建造一個(gè)垃圾處理廠,使得 對(duì)
對(duì) 、
、 所張角最大,試確定點(diǎn)
所張角最大,試確定點(diǎn) 的位置.
的位置.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com