
(12分)連續拋兩次質地均勻的骰子得到的點數分別為 和
和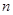 ,將
,將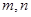 作為Q點的橫、縱坐標,
作為Q點的橫、縱坐標,
(1)記向量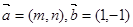 的夾角為
的夾角為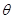 ,求
,求 的概率;
的概率;
(2)求點Q落在區域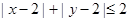 內的概率.
內的概率.
(1)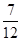 ;(2)
;(2)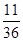 .
.
解析試題分析:(1)總的基本事件的個數有(1,1),(1,2),...,(6,6)共36個結果;
那么由于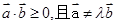 ,所以
,所以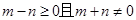 ,所以此事件包含的基本結果共有21個,
,所以此事件包含的基本結果共有21個,
所以此事件的概率為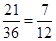 .
.
(2)作出不等式表示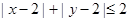 表示的平面區域可知是一個正方形,此正方形內包含橫縱坐標都為正整數的點有11個,所以其概率為
表示的平面區域可知是一個正方形,此正方形內包含橫縱坐標都為正整數的點有11個,所以其概率為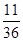 .
.
考點:向量的夾角,向量的數量積,線性規劃,古典概型概率.
點評:根據向量夾角的范圍可知向量的數量積大于零,據此可得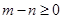 ,從而得到(1,1),(1,2),...(6,6)共36個點中有21個滿足,然后根據古典概型概率計算公式計算即可.
,從而得到(1,1),(1,2),...(6,6)共36個點中有21個滿足,然后根據古典概型概率計算公式計算即可.
第(2)問關鍵是正確作出不等式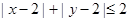 表示的平面區域可知是一個正方形,然后找出此正方形包括邊上的整點個數,再根據古典概型概率計算公式計算即可.
表示的平面區域可知是一個正方形,然后找出此正方形包括邊上的整點個數,再根據古典概型概率計算公式計算即可.


科目:高中數學 來源: 題型:解答題
甲、乙兩人各進行3次射擊,甲每次擊中目標的概率為 ,乙每次擊中目標的概率為
,乙每次擊中目標的概率為 ,兩人間每次射擊是否擊中目標互不影響。
,兩人間每次射擊是否擊中目標互不影響。
(1)求乙至多擊中目標2次的概率;
(2)求甲恰好比乙多擊中目標1次的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)
已知集合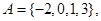 在平面直角坐標系中,點
在平面直角坐標系中,點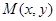 的橫、縱坐標滿足
的橫、縱坐標滿足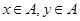 。
。
(1)請列出點 的所有坐標;
的所有坐標;
(2)求點 不在
不在 軸上的概率;
軸上的概率;
(3)求點 正好落在區域
正好落在區域 上的概率。
上的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題12分)現有甲、乙兩個靶.某射手向甲靶射擊一次,命中的概率為 ,命中得
,命中得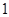 分,沒有命中得
分,沒有命中得 分;向乙靶射擊兩次,每次命中的概率為
分;向乙靶射擊兩次,每次命中的概率為 ,每命中一次得
,每命中一次得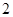 分,沒有命中得
分,沒有命中得 分.該射手每次射擊的結果相互獨立.假設該射手完成以上三次射擊.(1)求該射手恰好命中一次的概率;(2)求該射手的總得分
分.該射手每次射擊的結果相互獨立.假設該射手完成以上三次射擊.(1)求該射手恰好命中一次的概率;(2)求該射手的總得分 的分布列及數學期望
的分布列及數學期望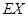 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分10分)某網站欲調查網民對當前網頁的滿意程度,在登錄的所有網民中,收回有效帖子共50000份,其中持各種態度的份數如下表所示.
| 很滿意 | 滿意 | 一般 | 不滿意 |
| 10800 | 12400 | 15600 | 11200 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分13分)在甲、乙兩個盒子中分別裝有標號為1、2、3、4的四個球,現從甲、乙兩個盒子中各取出1個球,每個小球被取出的可能性相等.
(1)求取出的兩個球上標號為相鄰整數的概率;
(2)求取出的兩個球上標號之和能被3整除的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在一個盒子中,放有標號分別為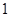 ,
,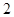 ,
, 的三張卡片,現從這個盒子中,有放回地先后抽得兩張卡片的標號分別為
的三張卡片,現從這個盒子中,有放回地先后抽得兩張卡片的標號分別為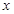 、
、 ,記
,記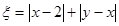 .
.
(Ⅰ)求隨機變量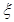 的最大值,并求事件“
的最大值,并求事件“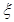 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求隨機變量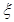 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com