
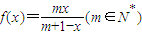
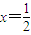 ,記
,記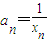 (n∈N*),求數列{an}的通項公式.
(n∈N*),求數列{an}的通項公式. ,由
,由 ,能夠證明f(x)∈A.
,能夠證明f(x)∈A. ,得
,得 .所以
.所以 ,因為
,因為 ,所以{an-1}是首項為
,所以{an-1}是首項為 ,公比為
,公比為 的等比數列.由此能求出數列{an}的通項公式.
的等比數列.由此能求出數列{an}的通項公式. ,
, ,
, ,
, ,
, .
. ,
, ,
, ,
, ,公比為
,公比為 的等比數列.
的等比數列. ,
, .
.

科目:高中數學 來源: 題型:
| mx |
| m+1-x |
| 1 |
| 2 |
| 1 |
| xn |
| 1 |
| 2 |
| 1 |
| xn |
查看答案和解析>>
科目:高中數學 來源: 題型:
| mx |
| m+1-x |
| 1 |
| 2 |
| 1 |
| xn |
查看答案和解析>>
科目:高中數學 來源: 題型:
| mx |
| m+1-x |
| 1 |
| 2 |
| 1 |
| xn |
| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年宣武區質量檢一)(14分)
根據定義在集合A上的函數y=![]() ,構造一個數列發生器,其工作原理如下:
,構造一個數列發生器,其工作原理如下:
① 輸入數據![]() ,計算出
,計算出![]() ;
;
② 若![]() ,則數列發生器結束工作;
,則數列發生器結束工作;
若![]() ,則輸出
,則輸出![]() ,并將
,并將![]() 反饋回輸入端,再計算出
反饋回輸入端,再計算出![]() 。并依此規律繼續下去。
。并依此規律繼續下去。
現在有![]() ,
,![]()
![]() 。
。
(1) 求證:對任意![]() ,此數列發生器都可以產生一個無窮數列
,此數列發生器都可以產生一個無窮數列![]() ;
;
(2) 若![]() ,記
,記![]()
![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(3) 在(2)得條件下,證明![]()
![]() 。
。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com