
如圖,在斜三棱柱 中,側面
中,側面 ,
,
 ,
, ,底面
,底面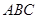 是邊長為
是邊長為 的正三角形,其重心為
的正三角形,其重心為 點,
點, 是線段
是線段 上一點,且
上一點,且 .
.
(1)求證: 側面
側面 ;
;
(2)求平面 與底面
與底面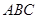 所成銳二面角的正切值.
所成銳二面角的正切值.
(1)證明:連接 并延長與
并延長與 交于
交于 點,則由題
點,則由題
意及相似關系可知點 為
為 的中點,所以
的中點,所以 三點共線,
三點共線,
從而可得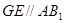 ,因此
,因此 側面
側面 ;
;
(2) .
.
解析試題分析:(1)要證明直線 側面
側面 ,即證明
,即證明 平行于側面
平行于側面 的某條直線,而由題意及相似關系易知
的某條直線,而由題意及相似關系易知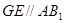 ,即可證明之;
,即可證明之;
(2)這問的關鍵是找出平面 與底面
與底面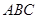 所成二面角的平面角,由側面
所成二面角的平面角,由側面 底面
底面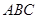 知,過
知,過 點作
點作 的垂線與
的垂線與 的延長線交于點
的延長線交于點 ,則
,則 平面
平面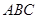 ,經過
,經過 點作
點作 的垂線與
的垂線與 的延長線交于點
的延長線交于點 ,則
,則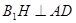 ,于是
,于是 即為所求二面角的平面角,然后根據相似關系可求該二面角的平面角的正切值.
即為所求二面角的平面角,然后根據相似關系可求該二面角的平面角的正切值.
試題解析:(1)證明:連接 并延長與
并延長與 交于
交于 點,則由題意及相似關系可知點
點,則由題意及相似關系可知點 為
為 的中點,
的中點,
所以 三點共線,從而可得
三點共線,從而可得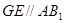 ,因此
,因此 側面
側面 .
.
(2)經過 點作
點作 的垂線與
的垂線與 的延長線交于點
的延長線交于點 ,則
,則 平面
平面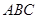 ,經過
,經過 點作
點作 的垂線與
的垂線與 的延長線交于點
的延長線交于點 ,則
,則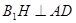 ,所以
,所以 即為所求二面角的平面角且
即為所求二面角的平面角且 ,則
,則 ,并由相似關系得:
,并由相似關系得: ,故
,故 ,即為所求二面角的正切值.
,即為所求二面角的正切值.
考點:與二面角有關的立體幾何綜合題;直線與平面平行的判定.


 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源: 題型:解答題
如圖,PDCE為矩形,ABCD為梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= CD=1,PD=
CD=1,PD= .
.
(1)若M為PA中點,求證:AC∥平面MDE;
(2)求直線PA與平面PBC所成角的正弦值;
(3)在線段PC上是否存在一點Q(除去端點),使得平面QAD與平面PBC所成銳二面角的大小為 ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在三棱錐P—ABC中,D,E,F分別為棱PC,AC,AB的中點.已知PA⊥AC,PA=6,BC=8,DF=5.
求證:(1)直線PA∥平面DFE;
(2)平面BDE⊥平面ABC.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知四邊形ABCD 是矩形,PA⊥平面ABCD,M, N分別是AB, PC的中點.
(1)求證:MN∥平面PAD;
(2)求證:MN⊥DC;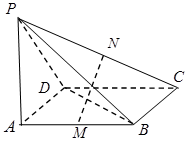
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱錐P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
(1)求證:PC⊥BC;
(2)求點A到平面PBC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知在空間四邊形ABCD中,E,F分別是AB,AD的中點,G,H分別是BC,CD上的點,且 =
= =2.求證:直線EG,FH,AC相交于一點.
=2.求證:直線EG,FH,AC相交于一點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com