
(本小題滿10分)設直線 的方程為
的方程為 .
.
(1) 若 在兩坐標軸上的截距相等,求
在兩坐標軸上的截距相等,求 的方程;
的方程;
(2) 若 不經過第二象限,求實數
不經過第二象限,求實數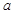 的取值范圍.
的取值范圍.
(1) 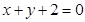 .(2) a≤-1.
.(2) a≤-1.
解析試題分析:
(Ⅰ)根據直線方程求出它在兩坐標軸上的截距,根據它在兩坐標軸上的截距相等,求出a的值,即得直線l方程.
(Ⅱ)把直線方程化為斜截式為 y=-(a+1)x-a-2,若l不經過第二象限,則a="-1" 或 -(a+1)》0,-a-2≤0,由此求得實數a的取值范圍。
解:(1)當直線過原點時,該直線在 軸和
軸和 軸上的截距都為零,截距相等,
軸上的截距都為零,截距相等,
∴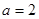 ,方程即
,方程即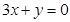 . ﹍﹍﹍﹍﹍﹍﹍2分
. ﹍﹍﹍﹍﹍﹍﹍2分
若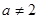 ,由于截距存在,∴
,由于截距存在,∴ 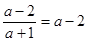 , ﹍﹍﹍﹍﹍﹍﹍3分
, ﹍﹍﹍﹍﹍﹍﹍3分
即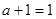 ,∴
,∴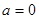 , 方程即
, 方程即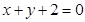 . ﹍﹍﹍﹍﹍﹍﹍﹍5分
. ﹍﹍﹍﹍﹍﹍﹍﹍5分
(2)法一:將 的方程化為
的方程化為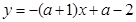 , ﹍﹍﹍﹍﹍﹍﹍﹍7分
, ﹍﹍﹍﹍﹍﹍﹍﹍7分
∴欲使 不經過第二象限,當且僅當
不經過第二象限,當且僅當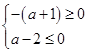 ﹍﹍﹍﹍﹍﹍﹍9分
﹍﹍﹍﹍﹍﹍﹍9分
∴a≤-1. 所以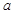 的取值范圍是a≤-1. ﹍﹍﹍﹍﹍﹍10分
的取值范圍是a≤-1. ﹍﹍﹍﹍﹍﹍10分
法二:將 的方程化為(x+y+2)+a(x-1)=0(a∈R), ﹍﹍﹍﹍﹍﹍﹍7分
的方程化為(x+y+2)+a(x-1)=0(a∈R), ﹍﹍﹍﹍﹍﹍﹍7分
它表示過l1:x+y+2=0與l2:x-1=0的交點(1,-3)的直線系(不包括x=1).由圖象可知l的斜率-(a+1)≥0時,l不經過第二象限,∴a≤-1. ﹍﹍﹍﹍﹍﹍﹍﹍10分
考點:本題主要考查直線方程的一般式,直線在坐標軸上的截距的定義,直線在坐標系中的位置與它的斜率、截距的關系,屬于基礎題
點評:解決該試題的易錯點是對于直線在坐標軸上截距相等的理解中,缺少過原點的情況的分析。


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:高中數學 來源: 題型:解答題
(本題滿分13分)已知光線經過已知直線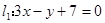 和
和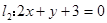 的交點
的交點 , 且射到
, 且射到 軸上一點
軸上一點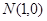 后被
后被 軸反射.
軸反射.
(1)求點 關于
關于 軸的對稱點
軸的對稱點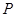 的坐標;
的坐標;
(2)求反射光線所在的直線 的方程.
的方程.
(3)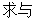

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在直角坐標系xOy中,曲線C1的點均在C2:(x-5)2+y2=9外,且對C1上任意一點M,M到直線x=﹣2的距離等于該點與圓C2上點的距離的最小值.
(Ⅰ)求曲線C1的方程;
(1-4班做)(Ⅱ)設P(x0,y0)(y0≠±3)為圓C2外一點,過P作圓C2的兩條切線,分別與曲線C1相交于點A,B和C,D.證明:當P在直線x=﹣4上運動時,四點A,B,C,D的縱坐標之積為定值.
(5-7班做)(Ⅱ)設P(-4,1)為圓C2外一點,過P作圓C2的兩條切線,分別與曲線C1相交于點A,B和C,D.證明:四點A,B,C,D的縱坐標之積為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com