
已知函數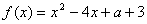 ,
,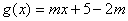 .
.
(1)若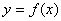 在
在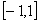 上存在零點,求實數
上存在零點,求實數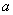 的取值范圍;
的取值范圍;
(2)當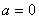 時,若對任意的
時,若對任意的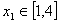 ,總存在
,總存在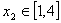 ,使
,使 ,求實數
,求實數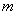 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:解答題
(本題滿分13分)
為了保護環境,某工廠在政府部門的支持下,進行技術改進: 把二氧化碳轉化為某種化工產品,經測算,該處理成本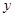 (萬元)與處理量
(萬元)與處理量 (噸)之間的函數關系可近似地表示為:
(噸)之間的函數關系可近似地表示為: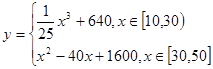 , 且每處理一噸二氧化碳可得價值為
, 且每處理一噸二氧化碳可得價值為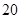 萬元的某種化工產品.
萬元的某種化工產品.
(Ⅰ)當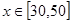 時,判斷該技術改進能否獲利?如果能獲利,求出最大利潤;如果不能獲利,則國家至少需要補貼多少萬元,該工廠才不虧損?
時,判斷該技術改進能否獲利?如果能獲利,求出最大利潤;如果不能獲利,則國家至少需要補貼多少萬元,該工廠才不虧損?
(Ⅱ) 當處理量為多少噸時,每噸的平均處理成本最少.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有一邊長為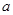 的正方形鐵片,鐵片的四角截去四個邊長為
的正方形鐵片,鐵片的四角截去四個邊長為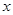 的小正方形,然后做成一個無蓋方盒。
的小正方形,然后做成一個無蓋方盒。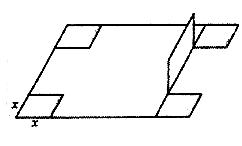
(1)試把方盒的容積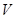 表示成
表示成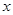 的函數;
的函數;
(2)求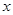 多大時,做成方盒的容積
多大時,做成方盒的容積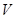 最大。
最大。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廠家擬在2010年舉行促銷活動,經調查測算,該產品的年銷售量(即該廠的年產量) 萬件與促銷費用
萬件與促銷費用 萬元(
萬元(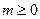 )滿足
)滿足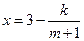 (
(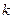 為常數),如果不搞促銷活動,則該產品的年銷量只能是1萬件。已知2010年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品的年平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金)。
為常數),如果不搞促銷活動,則該產品的年銷量只能是1萬件。已知2010年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品的年平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金)。
(1)將2010年該產品的利潤y萬元表示為年促銷費用m萬元的函數;
(2)該廠家2010年的促銷費用投入多少萬元時,廠家的利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)某新型智能在線電池的電量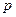 (單位:kwh)隨時間
(單位:kwh)隨時間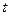 (單位:小時)的變化規律是:
(單位:小時)的變化規律是: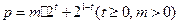 ,其中
,其中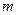 是智能芯片實時控制的參數。
是智能芯片實時控制的參數。
(1)當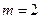 時,求經過多少時間電池電量是
時,求經過多少時間電池電量是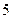 kwh;
kwh;
(2)如果電池的電量始終不低于2 kwh,求參數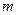 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)
已知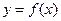 是定義在R上的偶函數,當
是定義在R上的偶函數,當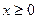 時,
時,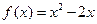
(1)求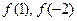 的值;
的值;
⑵求 的解析式并畫出簡圖;
的解析式并畫出簡圖;
⑶討論方程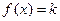 的根的情況。(只需寫出結果,不要解答過程).
的根的情況。(只需寫出結果,不要解答過程).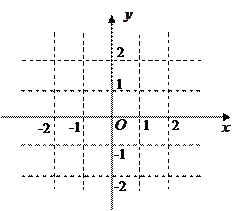
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分,第(1)小題7分,第(2)小題7分)
某地發生特大地震和海嘯,使當地的自來水受到了污染,某部門對水質檢測后,決定往水中投放一種藥劑來凈化水質。已 知每投放質量為
知每投放質量為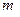 的藥劑后,經過
的藥劑后,經過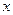 天該藥劑在水中釋放的濃度
天該藥劑在水中釋放的濃度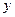 (毫克/升) 滿足
(毫克/升) 滿足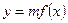 ,其中
,其中 ,當藥劑在水中釋放的濃度不低于
,當藥劑在水中釋放的濃度不低于 (毫克/升)時稱為有效凈化;當藥劑在水中釋放的濃度不低于
(毫克/升)時稱為有效凈化;當藥劑在水中釋放的濃度不低于 (毫克/升) 且不高于10(毫克/升)時稱為最佳凈化。
(毫克/升) 且不高于10(毫克/升)時稱為最佳凈化。
(1)如果投放的藥劑質量為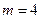 ,試問自來水達到有效凈化一共可持續幾天?
,試問自來水達到有效凈化一共可持續幾天?
(2)如果投放的藥劑質量為 ,為了使在7天之內(從投放藥劑算起包括7天)的自來水達到最佳凈化,試確定應該投放的藥劑質量
,為了使在7天之內(從投放藥劑算起包括7天)的自來水達到最佳凈化,試確定應該投放的藥劑質量 的值。
的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com