
甲、乙兩名同學參加“漢字聽寫大賽”選拔測試,在相同測試條件下,兩人5次測試的成績(單位:分)如下表: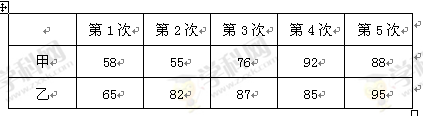
(Ⅰ)請畫出甲、乙兩人成績的莖葉圖. 你認為選派誰參賽更好?說明理由(不用計算);
(Ⅱ)若從甲、乙兩人5次的成績中各隨機抽取一個成績進行分析,設抽到的兩個成績中,90分以上的個數為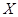 ,求隨機變量
,求隨機變量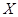 的分布列和期望
的分布列和期望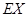 .
.
(Ⅰ)選派乙參賽更好(Ⅱ)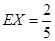
解析試題分析:(Ⅰ)莖表示得分的十位數,放在中間的列,葉表示得分的個位數,放在兩側。從莖葉圖可觀察出甲的得分比較分散,乙得分比較集中即波動小、相對穩定,所以應選派乙參賽更好。(Ⅱ)本題容易將基本事件總數記為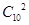 ,應注意審題,要求是從兩人5次的成績中各隨機抽取一個成績,強調一個“各”字,所以基本事件總數為
,應注意審題,要求是從兩人5次的成績中各隨機抽取一個成績,強調一個“各”字,所以基本事件總數為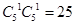 。抽到的兩個成績中90分以上的事件包含的基本事件總數也應各自抽取,然后根據古典概型概率公式
。抽到的兩個成績中90分以上的事件包含的基本事件總數也應各自抽取,然后根據古典概型概率公式 求其概率。根據各自概率繪制隨機變量
求其概率。根據各自概率繪制隨機變量 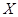 的分布列,再根據期望公式
的分布列,再根據期望公式 求期望。
求期望。
試題解析:
解:(Ⅰ)莖葉圖如上圖所示,由圖可知,乙的平均成績大于甲的平均成績,且乙的方差小于甲的方差,因此應. 6分
(Ⅱ)隨機變量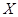 的所有可能取值為
的所有可能取值為 .
.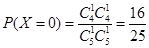 ,
,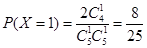 ,
,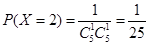 ,
,
隨機變量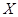 的分布列是:
的分布列是: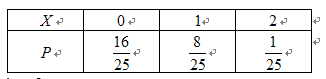
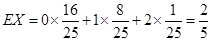 . 13分
. 13分
考點:1.莖葉圖;2.離散型隨機變量及其分布列


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:解答題
某高中為了推進新課程改革,滿足不同層次學生的需求,決定從高一年級開始,在每周的周一、周三、周五的課外活動期間同時開設數學、物理、化學、生物和信息技術輔導講座,每位有興趣的同學可以在期間的任何一天參加任何一門科目的輔導講座,也可以放棄任何一門科目的輔導講座。(規定:各科達到預先設定的人數時稱為滿座,否則稱為不滿座)統計數據表明,各學科講座各天的滿座的概率如下表: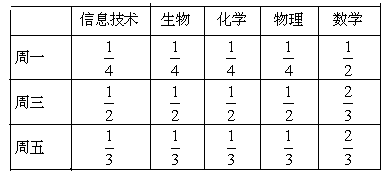
根據上表:
(1)求數學輔導講座在周一、周三、周五都不滿座的概率;
(2)設周三各輔導講座滿座的科目數為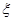 ,求隨機變量
,求隨機變量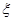 的分布列和數學期望。
的分布列和數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某牛奶廠要將一批牛奶用汽車從所在城市甲運至城市乙,已知從城市甲到城市乙只有兩條公路,且運費由廠商承擔.若廠商恰能在約定日期(×月×日)將牛奶送到,則城市乙的銷售商一次性支付給牛奶廠20萬元;若在約定日期前送到,每提前一天銷售商將多支付給牛奶廠1萬元;若在約定日期后送到,每遲到一天銷售商將少支付給牛奶廠1萬元.為保證牛奶新鮮度,汽車只能在約定日期的前兩天出發,且只能選擇其中的一條公路運送牛奶,已知下表內的信息:
| 統計信息 汽車行駛路線 | 在不堵車的情況下到達城市乙所需時間(天) | 在堵車的情況下到達城市乙所需時間(天) | 堵車的概率 | 運費(萬元) |
| 公路1 | 2 | 3 | 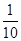 | 1.6 |
| 公路2 | 1 | 4 | 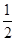 | 0.8 |
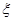 (單位:萬元),求
(單位:萬元),求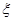 的分布列和數學期望
的分布列和數學期望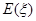 ;
;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市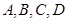 四所中學報名參加某高校今年自主招生的學生人數如下表所示:
四所中學報名參加某高校今年自主招生的學生人數如下表所示:
| 中學 | 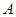 |  | 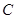 | 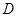 |
| 人數 | 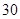 | 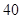 | 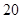 | 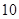 |
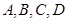 四所中學各抽取多少名學生?
四所中學各抽取多少名學生?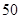 名學生中隨機抽取兩名學生,求這兩名學生自同一所中學的概率;
名學生中隨機抽取兩名學生,求這兩名學生自同一所中學的概率;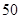 名學生中,從自
名學生中,從自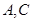 兩所中學的學生當中隨機抽取兩名學
兩所中學的學生當中隨機抽取兩名學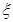 表示抽得
表示抽得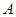 中學的學生人數,求
中學的學生人數,求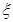 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
生產A,B兩種元件,其質量按測試指標劃分為:指標大于或等于82為正品,小于82為
次品,現隨機抽取這兩種元件各100件進行檢測,檢測結果統計如下:
| 測試指標 | 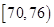 | 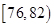 | 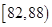 | 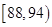 | 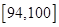 |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學經市批準建設分校,工程從2010年底開工到2013年底完工,分三期完成,經過初步招標淘汰后,確定由甲、乙兩建筑公司承建,且每期工程由兩公司之一獨立完成,必須在建完前一期工程后再建后一期工程,已知甲公司獲得第一期,第二期,第三期工程承包權的概率分別是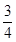 ,
,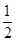 ,
,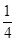 .
.
(I)求甲乙兩公司均至少獲得l期工程的概率;
(II)求甲公司獲得的工程期數的分布列和數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一中食堂有一個面食窗口,假設學生買飯所需的時間互相獨立,且都是整數分鐘,對以往學生買飯所需的時間統計結果如下:
| 買飯時間(分) | 1 | 2 | 3 | 4 | 5 |
| 頻率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
 表示至第2分鐘末已買完飯的人數,求
表示至第2分鐘末已買完飯的人數,求 的分布列及數學期望
的分布列及數學期望查看答案和解析>>
科目:高中數學 來源: 題型:解答題
氣象部門提供了某地今年六月份(30天)的日最高氣溫的統計表如下:
| 日最高氣溫t (單位:℃) | t 22℃ 22℃ | 22℃< t 28℃ 28℃ | 28℃< t  32℃ 32℃ | 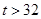 ℃ ℃ |
| 天數 | 6 | 12 |  |  |
 和
和 數據不清楚,但氣象部門提供的資料顯示,六月份的日最高氣溫不高于32℃的頻率為0.9.
數據不清楚,但氣象部門提供的資料顯示,六月份的日最高氣溫不高于32℃的頻率為0.9. ,
, 的值;
的值;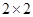 列聯表,并據此你是否有95%的把握認為本地區的“高溫天氣”與西瓜“旺銷”有關?說明理由.
列聯表,并據此你是否有95%的把握認為本地區的“高溫天氣”與西瓜“旺銷”有關?說明理由.| | 高溫天氣 | 非高溫天氣 | 合計 |
| 旺銷 | 1 | | |
| 不旺銷 | | 6 | |
| 合計 | | | |

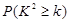 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為貫徹“激情工作,快樂生活”的理念,某單位在工作之余舉行趣味知識有獎競賽,比賽分初賽和決賽兩部分.為了增加節目的趣味性,初賽采用選手選一題答一題的方式進行,每位選手最多有5次選題答題的機會,選手累計答對3題或答錯3題即終止其初賽的比賽,答對3題者直接進入決賽,答錯3題者則被淘汰.已知選手甲答題的正確率為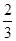 .
.
(1)求選手甲答題次數不超過4次可進入決賽的概率;
(2)設選手甲在初賽中答題的個數為X,試寫出X的分布列,并求X的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com