
氣象部門提供了某地今年六月份(30天)的日最高氣溫的統計表如下:
| 日最高氣溫t (單位:℃) | t 22℃ 22℃ | 22℃< t 28℃ 28℃ | 28℃< t  32℃ 32℃ | 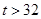 ℃ ℃ |
| 天數 | 6 | 12 |  |  |
 和
和 數據不清楚,但氣象部門提供的資料顯示,六月份的日最高氣溫不高于32℃的頻率為0.9.
數據不清楚,但氣象部門提供的資料顯示,六月份的日最高氣溫不高于32℃的頻率為0.9. ,
, 的值;
的值;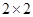 列聯表,并據此你是否有95%的把握認為本地區的“高溫天氣”與西瓜“旺銷”有關?說明理由.
列聯表,并據此你是否有95%的把握認為本地區的“高溫天氣”與西瓜“旺銷”有關?說明理由.| | 高溫天氣 | 非高溫天氣 | 合計 |
| 旺銷 | 1 | | |
| 不旺銷 | | 6 | |
| 合計 | | | |

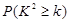 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(Ⅰ)9,3;(Ⅱ)沒有95%的把握認為本地區的“高溫天氣”與西瓜 “旺銷”有關.
解析試題分析:(Ⅰ)把頻率看作概率,
科目:高中數學
來源:
題型:解答題
甲、乙兩名同學參加“漢字聽寫大賽”選拔測試,在相同測試條件下,兩人5次測試的成績(單位:分)如下表:
科目:高中數學
來源:
題型:解答題
為貫徹“激情工作,快樂生物”的理念,某單位在工作之余舉行趣味知識有獎競賽,比賽分初賽和決賽兩部分,為了增加節目的趣味性,初賽采用選手選—題答—題的方式進行,每位選手最多有5次選答題的機會,選手累計答對3題或答錯3題即終止其初賽的比賽,答對3題者直接進入決賽,答錯3題者則被淘汰,已知選手甲答題的正確率為
科目:高中數學
來源:
題型:解答題
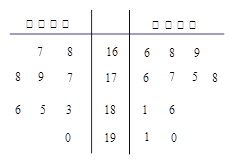
學校為了使運動員順利參加運動會,招募了8名男志愿者和12名女志愿者,這20名志愿者的身高如下莖葉圖(單位:cm):若身高在180cm以上(包括180cm)定義為“高個子”,身高在180cm以下(不包括180cm)定義為“非高個子”,且只有“女高個子”才能擔任“禮儀小姐”.
科目:高中數學
來源:
題型:解答題
某社區舉辦防控甲型H7N9流感知識有獎問答比賽,甲、乙、丙三人同時回答一道衛生知識題,三人回答正確與錯誤互不影響。已知甲回答這題正確的概率是
科目:高中數學
來源:
題型:解答題
省少年籃球隊要從甲、乙兩所體校選拔隊員。現將這兩所體校共20名學生的身高繪制成如下莖葉圖(單位:cm):若身高在180cm以上(包括180cm)定義為“高個子”,身高在180cm以下(不包括180cm)定義為“非高個子”.
科目:高中數學
來源:
題型:解答題
某飲料公司對一名員工進行測試以便確定其考評級別.公司準備了兩種不同的飲料共5 杯,其顏色完全相同,并且其中3杯為
科目:高中數學
來源:
題型:解答題
小王經營一家面包店,每天從生產商處訂購一種品牌現烤面包出售.已知每賣出一個現烤面包可獲利10元,若當天賣不完,則未賣出的現烤面包因過期每個虧損5元.經統計,得到在某月(30天)中,小王每天售出的現烤面包個數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區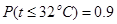 ,根據頻率和為1,可求得
,根據頻率和為1,可求得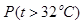 ,在由皮書等于頻率
,在由皮書等于頻率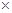 樣本總數,便求得
樣本總數,便求得 ,
,  的值;(Ⅱ)利用
的值;(Ⅱ)利用 求出
求出 的觀測值,把
的觀測值,把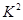 的值與臨界值比較,如下表:確定
的值與臨界值比較,如下表:確定 與
與 有關系的程度或無關系.
有關系的程度或無關系.
若P(k2>k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828  ,則有95℅的把握說明兩個事件有關;
,則有95℅的把握說明兩個事件有關;
若 ,則有99℅的把握說明兩個事件有關;
,則有99℅的把握說明兩個事件有關;
若 ,則沒有理由認為兩個事件有關.
,則沒有理由認為兩個事件有關.
試題解析:(Ⅰ)由已知的: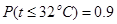 ,
,
∴  ,
,
∴ 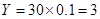 ,
,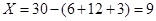 . 6分
. 6分
(Ⅱ) 高溫天氣 非高溫天氣 合 計 旺銷<


西城學科專項測試系列答案
小考必做系列答案
小考實戰系列答案
小考復習精要系列答案
小考總動員系列答案
小升初必備沖刺48天系列答案
68所名校圖書小升初高分奪冠真卷系列答案
伴你成長周周練月月測系列答案
小升初金卷導練系列答案
萌齊小升初強化模擬訓練系列答案
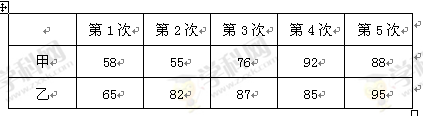
(Ⅰ)請畫出甲、乙兩人成績的莖葉圖. 你認為選派誰參賽更好?說明理由(不用計算);
(Ⅱ)若從甲、乙兩人5次的成績中各隨機抽取一個成績進行分析,設抽到的兩個成績中,90分以上的個數為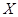 ,求隨機變量
,求隨機變量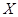 的分布列和期望
的分布列和期望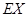 .
. .
.
(1)求選手甲答題次數不超過4次可進入決賽的概率;
(2)設選手甲在初賽中答題的個數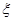 ,試寫出
,試寫出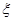 的分布列,并求
的分布列,并求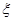 的數學期望。
的數學期望。
(Ⅰ)用分層抽樣的方法從“高個子”和“非高個子”中抽取5人,如果從這5人中隨機選2人,那么至少有1人是“高個子”的概率是多少?男 女 8 16 5 8 9 8 7 6 17 2 3 5 5 6 7 4 2 18 0 1 2 1 19 0
(Ⅱ)若從所有“高個子”中隨機選3名志愿者,用 表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出
表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出 的分布列,并求
的分布列,并求 的數學期望.
的數學期望. ,甲、丙兩人都回答錯誤的概率是
,甲、丙兩人都回答錯誤的概率是 ,乙、丙兩人都回答正確的概率是
,乙、丙兩人都回答正確的概率是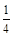 .
.
(I)求乙、丙兩人各自回答這道題正確的概率;
(II)用 表示回答該題正確的人數,求
表示回答該題正確的人數,求 的分布列和數學期望
的分布列和數學期望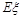 .
.
(1)用分層抽樣的方法從“高個子”和“非高個子”中抽取5人,如果從這5人中隨
機選2人,那么至少有一人是“高個子”的概率是多少?
(2)從兩隊的“高個子”中各隨機抽取1人,求恰有1人身高達到190cm的概率.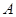 飲料,另外2杯為
飲料,另外2杯為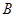 飲料,公司要求此員工一一品嘗后,從5杯飲料中選出3杯
飲料,公司要求此員工一一品嘗后,從5杯飲料中選出3杯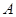 飲料.若該員工3杯都選對,則評為優秀;若3杯選對2杯,則評為良好;否則評為及格.假設此人對
飲料.若該員工3杯都選對,則評為優秀;若3杯選對2杯,則評為良好;否則評為及格.假設此人對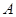 和
和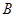 兩種飲料沒有鑒別能力.
兩種飲料沒有鑒別能力.
(Ⅰ)求此人被評為優秀的概率;
(Ⅱ)求此人被評為良好及以上的概率. 及天數如下表:
及天數如下表:
試依據以頻率估計概率的統計思想,解答下列問題:售出個數 
10 11 12 13 14 15 天數 3 3 3 6 9 6
(Ⅰ)計算小王某天售出該現烤面包超過13個的概率;
(Ⅱ)若在今后的連續5天中,售出該現烤面包超過13個的天數大于3天,則小王決定增加訂購量. 試求小王增加訂購量的概率.
(Ⅲ)若小王每天訂購14個該現烤面包,求其一天出售該現烤面包所獲利潤的分布列和數學期望.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號