
平面內有n(n∈N+,n≥2)條直線,其中任何兩條不平行,任何三條不過
同一點,證明:交點的個數f(n)= .
.
見解析
【解析】(1)當n=2時,兩條直線的交點只有一個,
又f(2)=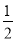 ×2×(2-1)=1,
×2×(2-1)=1,
∴當n=2時,命題成立.
(2)假設n=k,∈N+,且(k>2)時,命題成立,即平面內滿足題設的任何k條直線交點個數f(k)=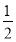 k(k-1),
k(k-1),
那么,當n=k+1時,任取一條直線l,除l以外其他k條直線交點個數為f(k)=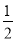 k(k-1),l與其他k條直線交點個數為k,從而k+1條直線共有f(k)+k個交點,
k(k-1),l與其他k條直線交點個數為k,從而k+1條直線共有f(k)+k個交點,
即f(k+1)=f(k)+k=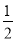 k(k-1)+k=
k(k-1)+k=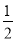 k(k-1+2)=
k(k-1+2)=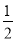 k(k+1)=
k(k+1)=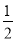 (k+1)[(k+1)-1],
(k+1)[(k+1)-1],
這表明,當n=k+1時,命題成立.
由(1)、(2)可知,對n∈N+(n≥2)命題都成立.


 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源:2015屆遼寧省沈陽市高二質量監測文科數學試卷(解析版) 題型:選擇題
若一個動點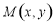 到兩個定點
到兩個定點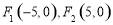 的距離之差的絕對值等于8,則動點M的軌跡方程為 ( )
的距離之差的絕對值等于8,則動點M的軌跡方程為 ( )
A.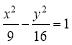 B.
B.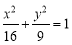
C.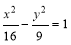 D.
D.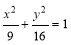
查看答案和解析>>
科目:高中數學 來源:2015屆遼寧大連普通高中高二上學期期末考試文數學卷(解析版) 題型:選擇題
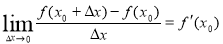 ,其中
,其中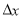 ( )
( )
(A)恒取正值或恒取負值 (B)有時可以取0
(C)恒取正值 (D)可以取正值和負值,但不能取0
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標6章末練習卷(解析版) 題型:選擇題
某個命題與正整數有關,如果當n=k(k∈N+)時,該命題成立,那么可
推得當n=k+1時命題也成立.現在已知當n=5時,該命題不成立,那么可推得( ).
A.當n=6時該命題不成立
B.當n=6時該命題成立
C.當n=4時該命題不成立
D.當n=4時該命題成立
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標6.3練習卷(解析版) 題型:解答題
已知,n∈N+,An=2n2,Bn=3n,試比較An與Bn的大小,
并加以證明.
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標6.2練習卷(解析版) 題型:填空題
已知函數f(x)在[0,1]上有意義,且f(0)=f(1),如果對任意的x1,x2∈[0,1]
且x1≠x2,都有|f(x1)-f(x2)|<|x1-x2|,求證:|f(x1)-f(x2)|<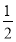 ,若用反證法證明該題,則反設應為________.
,若用反證法證明該題,則反設應為________.
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標6.1練習卷(解析版) 題型:解答題
在數列{an}中,a1=1,an+1=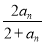 ,n∈N+,求a2,a3,a4
,n∈N+,求a2,a3,a4
并猜想數列的通項公式,并給出證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com