
已知函數 (
(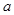 是常數且
是常數且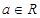 )
)
(1)若函數 的一個零點是1,求
的一個零點是1,求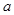 的值;
的值;
(2)求 在
在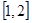 上的最小值
上的最小值 ;
;
(3)記 若
若 ,求實數
,求實數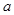 的取值范圍。
的取值范圍。
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析試題分析:(1)因為1是 的一個零點,將1代入得
的一個零點,將1代入得 ,求得
,求得 ;(2)由題意
;(2)由題意 ,先討論二次項系數
,先討論二次項系數 ,得最小值
,得最小值 ,然后討論對稱軸
,然后討論對稱軸 分別位于區間
分別位于區間 的各種情況,求出
的各種情況,求出 的最小值,合并得到
的最小值,合并得到 的最小值
的最小值 ,注意分類討論時不重不漏;(3)由題意
,注意分類討論時不重不漏;(3)由題意 即相當于
即相當于 恒成立,分離參數即可得
恒成立,分離參數即可得 恒成立,令
恒成立,令 ,
, ,分
,分 求得
求得 的最大值為
的最大值為 ,所以
,所以 .
.
試題解析:(1)由題意知 2分
2分
(2)
 ⅰ當
ⅰ當 時
時 3分
3分
ⅱ當 時,對稱軸為
時,對稱軸為
 4分
4分
ⅲ當 時,拋物線開口向下,對稱軸
時,拋物線開口向下,對稱軸
若 即
即 時,
時,
若 即
即 時,
時,
若 即
即 時,
時, 7分
7分
綜上所述, 8分
8分
(3)由題意知:不等式 無解
無解
即 恒成立 10分
恒成立 10分
即 對任意
對任意 恒成立 11分
恒成立 11分
令 則
則 對任意
對任意 恒成立12分
恒成立12分
ⅰ當 時
時 13分
13分
ⅱ當 時
時 14分
14分
ⅲ當 時
時
 15分
15分 即
即 16分
16分
考點:1、函數的零點;2、二次函數在給定區間上的最值;3、分離參數處理恒成立問題;4、分類討論思想.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
方便、快捷、實惠的電動車是很多人的出行工具。可是,隨著電動車的普及,它的安全性也越來越受到人們關注。為了出行更安全,交通部門限制電動車的行駛速度為24km/h。若某款電動車正常行駛遇到緊急情況時,緊急剎車時行駛的路程S(單位:m)和時間t(單位:s)的關系為: 。
。
(Ⅰ)求從開始緊急剎車至電動車完全停止所經過的時間;
(Ⅱ)求該款車正常行駛的速度是否在限行范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知偶函數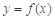 滿足:當
滿足:當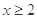 時,
時,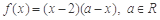 ,當
,當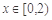 時,
時,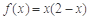 .
.
(1)求當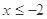 時,
時,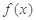 的表達式;
的表達式;
(2)試討論:當實數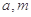 滿足什么條件時,函數
滿足什么條件時,函數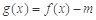 有4個零點,且這4個零點從小到大依次構成等差數列.
有4個零點,且這4個零點從小到大依次構成等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一種放射性元素,最初的質量為 ,按每年
,按每年 衰減.
衰減.
(1)求 年后,這種放射性元素的質量
年后,這種放射性元素的質量 與
與 的函數關系式;
的函數關系式;
(2)求這種放射性元素的半衰期(質量變為原來的 時所經歷的時間).(
時所經歷的時間).( )
)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在不考慮空氣阻力的情況下,火箭的最大速度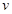 (單位:
(單位: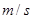 )和燃料的質量
)和燃料的質量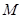 (單位:
(單位: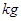 ),火箭(除燃料外)的質量
),火箭(除燃料外)的質量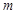 (單位:
(單位: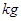 )滿足
)滿足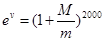 .(
.(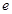 為自然對數的底)
為自然對數的底)
(Ⅰ)當燃料質量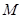 為火箭(除燃料外)質量
為火箭(除燃料外)質量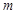 兩倍時,求火箭的最大速度(單位:
兩倍時,求火箭的最大速度(單位: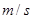 );
);
(Ⅱ)當燃料質量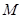 為火箭(除燃料外)質量
為火箭(除燃料外)質量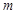 多少倍時,火箭的最大速度可以達到8
多少倍時,火箭的最大速度可以達到8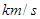 .(結果精確到個位,數據:
.(結果精確到個位,數據: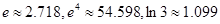 )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com