
(滿分14分)設函數 .若方程
.若方程 的根為0和2,且
的根為0和2,且 .
.
(1). 求函數 的解析式;
的解析式;
(2) 已知各項均不為零的數列 滿足:
滿足: 為該數列的前n項和),求該數列的通項
為該數列的前n項和),求該數列的通項 ;
;
(3)如果數列 滿足
滿足 .求證:當
.求證:當 時,恒有
時,恒有 成立.
成立.
科目:高中數學 來源: 題型:
(本題滿分14分)設函數![]()
(I)求函數![]() 的最小正周期及函數的單調遞增區間 ; (II)若
的最小正周期及函數的單調遞增區間 ; (II)若![]() ,是否存在實數m,使函數
,是否存在實數m,使函數![]() ?若存在,請求出m的取值;若不存在,請說明理由。
?若存在,請求出m的取值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)設函數![]() 的圖象與x軸相交于一點
的圖象與x軸相交于一點![]() ,且在點
,且在點![]() 處的切線方程是
處的切線方程是![]()
(I)求t的值及函數![]() 的解析式;
的解析式;
(II)設函數![]()
(1)若![]() 的極值存在,求實數m的取值范圍。
的極值存在,求實數m的取值范圍。
(2)假設![]() 有兩個極值點
有兩個極值點![]() 的表達式
的表達式![]() 并判斷
并判斷![]() 是否有最大值,若有最大值求出它;若沒有最大值,說明理由。
是否有最大值,若有最大值求出它;若沒有最大值,說明理由。
查看答案和解析>>
科目:高中數學 來源:2010年廣州市高二第二學期期末考試數學(文)試題 題型:解答題
(本題滿分14分)
設函數 ,
, ,當
,當 時,
時,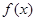 取得極值。
取得極值。
(Ⅰ)求 的值;
的值;
(Ⅱ)當 時,函數
時,函數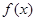 與
與 的圖象有三個公共點,求
的圖象有三個公共點,求 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com