
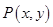 為函數
為函數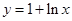 圖象上一點,O為坐標原點,記直線
圖象上一點,O為坐標原點,記直線 的斜率
的斜率 .
.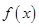 在區間
在區間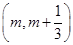
 上存在極值,求實數m的取值范圍;
上存在極值,求實數m的取值范圍;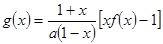 ,若對任意
,若對任意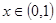 恒有
恒有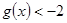 ,求實數
,求實數 的取值范圍.
的取值范圍. ;(2)
;(2) .
. ,先求其導數,令
,先求其導數,令 ,求出其導數為0的
,求出其導數為0的 值,然后判斷
值,然后判斷 兩側的單調性是否發生改變,求出極值點,讓極值點落在
兩側的單調性是否發生改變,求出極值點,讓極值點落在 ,即可求出
,即可求出 的范圍;
的范圍; ,
, 是負數,所以討論當
是負數,所以討論當 ,
,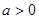 的情況;恒有
的情況;恒有 ,設
,設 ,求
,求 ,設
,設 ,由
,由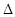 來確定
來確定 的范圍,來確定
的范圍,來確定 的正負,即
的正負,即 的正負,從而確定
的正負,從而確定 的單調性,如果
的單調性,如果 恒成立,只需
恒成立,只需 的最大值小于0,從而求出a的范圍.
的最大值小于0,從而求出a的范圍. ,
,
 2分
2分 時,
時, ;當
;當 時,
時, .所以
.所以 在
在 上單調遞增,在
上單調遞增,在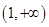 上單調遞減,故
上單調遞減,故 在
在 處取得極大值.
處取得極大值. 在區間
在區間 (其中
(其中 )上存在極值,
)上存在極值, ,得
,得 .即實數
.即實數 的取值范圍是
的取值范圍是 . 4分
. 4分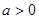 ,因為
,因為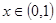 ,所以
,所以 .當
.當 時,
時, ,不合題意.
,不合題意. 時,由
時,由 ,
, 可得
可得 . 6分
. 6分 ,則.
,則.
 ,
, . 8分
. 8分 ,則
,則 ,
, ,
, ,所以
,所以 在
在 內單調遞增,又
內單調遞增,又 所以
所以 .所以
.所以 符合條件. 10分
符合條件. 10分 ,則
,則 ,
, ,
, ,所以存在
,所以存在 ,使得
,使得 ,對.則
,對.則 在
在 內單調遞減,又
內單調遞減,又 ,所以當
,所以當
 時,
時, ,不合要求.
,不合要求. . 12分
. 12分

科目:高中數學 來源:不詳 題型:解答題
 元(
元( )時,一年的銷售量為
)時,一年的銷售量為 萬件。
萬件。查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 ,
, .
. 在其定義域上為增函數,求
在其定義域上為增函數,求 的取值范圍;
的取值范圍; 時,函數
時,函數 在區間
在區間 上存在極值,求
上存在極值,求 的最大值.
的最大值. ≈
≈ ).
).查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.150 |
| B.175 |
| C.200 |
| D.225 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com