
已知數列{  }、{
}、{ 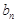 }滿足:
}滿足: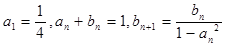 .
.
(1)求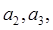
(2)證明:數列{ }為等差數列,并求數列
}為等差數列,并求數列 和{
和{ 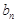 }的通項公式;
}的通項公式;
(3)設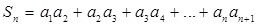 ,求實數
,求實數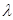 為何值時
為何值時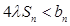 恒成立.
恒成立.
(1)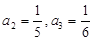 ;(2)
;(2)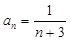 ,
,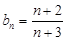 ;
;
解析試題分析:(1)由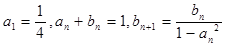 ,
,
可求出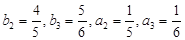 ;
;
(2)扣住等差數列的定義,從定義出發進行證明,
利用條件推導出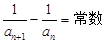 ,即得證:
,即得證:
∵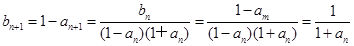
∴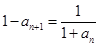 ,
,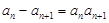
∴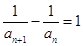
∴ 數列{ }是以4為首項,1為公差的等差數列
}是以4為首項,1為公差的等差數列
∴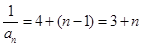
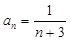 ∴
∴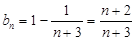
(3)借助前兩問,利用裂項求和法,可得出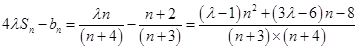 ,問題轉化為
,問題轉化為
設f(n)= 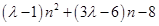 <0,恒成立問題,
<0,恒成立問題,
對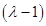 進行討論,分三種情況,從而可得出答案,見詳解.
進行討論,分三種情況,從而可得出答案,見詳解.
試題解析:(1) ∵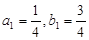 ∴
∴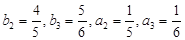
(2)∵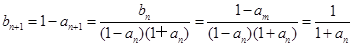
∴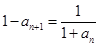 ,
,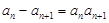
∴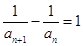 ,
,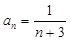 ∴
∴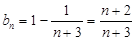
∴ 數列{ }是以4為首項,1為公差的等差數列
}是以4為首項,1為公差的等差數列
∴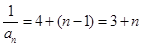
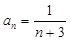 ∴
∴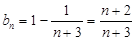
(3)已知 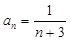 ,所以
,所以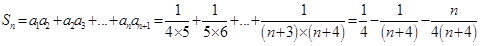
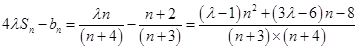
由條件可知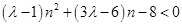 恒成立即可滿足條件.
恒成立即可滿足條件.
設f(n)= 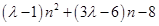
當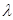 =1時,f(n)=-3n-8<0恒成立;
=1時,f(n)=-3n-8<0恒成立;
當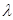 >1時,由二次函數的性質知不可能成立;
>1時,由二次函數的性質知不可能成立;
當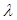 <1時,對稱軸
<1時,對稱軸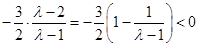 ,f(1)在
,f(1)在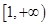 為單調遞減函數,
為單調遞減函數,
f(1)= 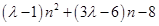 =
=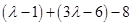 =4
=4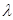 -15<0
-15<0
所以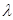 <
<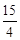
所以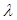 <1時
<1時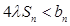 恒成立
恒成立
綜上知,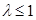 時 ,
時 ,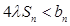 恒成立 .
恒成立 .
考點:等差數列,等比數列,二次函數,分類討論.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
已知數列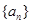 是等差數列,
是等差數列,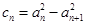 (
( ).
).
(Ⅰ)判斷數列 是否是等差數列,并說明理由;
是否是等差數列,并說明理由;
(Ⅱ)如果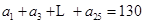 ,
, (
( 為常數),試寫出數列
為常數),試寫出數列 的通項公式;
的通項公式;
(Ⅲ)在(Ⅱ)的條件下,若數列 得前
得前 項和為
項和為 ,問是否存在這樣的實數
,問是否存在這樣的實數 ,使
,使 當且僅當
當且僅當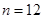 時取得最大值.若存在,求出
時取得最大值.若存在,求出 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列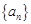 的前
的前 項和為
項和為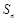 ,
,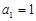 ,
, 是
是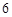 與
與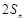 的等差中項(
的等差中項(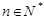 ).
).
(1)求數列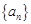 的通項公式;
的通項公式;
(2)是否存在正整數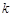 ,使不等式
,使不等式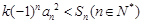 恒成立,若存在,求出
恒成立,若存在,求出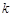
的最大值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com