
設(shè)函數(shù) 定義域為
定義域為 .
.
(1)若 ,求實數(shù)
,求實數(shù) 的取值范圍;
的取值范圍;
(2)若 在
在 上恒成立,求實數(shù)
上恒成立,求實數(shù) 的取值范圍.
的取值范圍.
(1)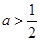 ,(2)
,(2)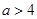 .
.
解析試題分析:(1)因為 ,所以
,所以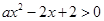 在
在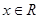 上恒成立. ① 當(dāng)
上恒成立. ① 當(dāng)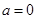 時,由
時,由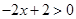 ,得
,得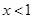 ,不成立,舍去,② 當(dāng)
,不成立,舍去,② 當(dāng)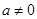 時,由
時,由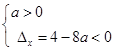 ,得
,得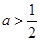 ,綜上所述,實數(shù)
,綜上所述,實數(shù) 的取值范圍是
的取值范圍是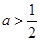 .(2))恒成立問題一般利用變量分離法轉(zhuǎn)化為最值問題. 依題有
.(2))恒成立問題一般利用變量分離法轉(zhuǎn)化為最值問題. 依題有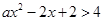 在
在 上恒成立,所以
上恒成立,所以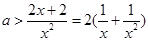 在
在 上恒成立, 令
上恒成立, 令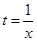 ,則由
,則由 ,得
,得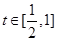 ,記
,記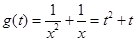 ,由于
,由于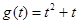 在
在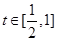 上單調(diào)遞增, 所以
上單調(diào)遞增, 所以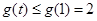 ,
, 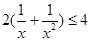
因此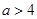
試題解析:解:(1)因為 ,所以
,所以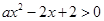 在
在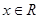 上恒成立. 2分
上恒成立. 2分
① 當(dāng)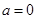 時,由
時,由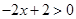 ,得
,得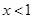 ,不成立,舍去, 4分
,不成立,舍去, 4分
② 當(dāng)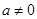 時,由
時,由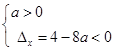 ,得
,得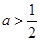 , 6分
, 6分
綜上所述,實數(shù) 的取值范圍是
的取值范圍是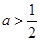 . 8分
. 8分
(2)依題有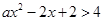 在
在 上恒成立, 10分
上恒成立, 10分
所以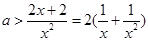 在
在 上恒成立, 12分
上恒成立, 12分
令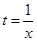 ,則由
,則由 ,得
,得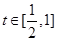 ,
,
記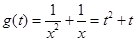 ,由于
,由于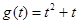 在
在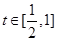 上單調(diào)遞增,
上單調(diào)遞增,
所以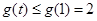 ,
, 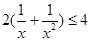
因此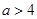 16分
16分
(使用函數(shù)在定義區(qū)間上最小值大于0求解可參照給分)
考點:不等式恒成立問題



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,ABCD是正方形空地,邊長為30m,電源在點P處,點P到邊AD、AB距離分別為9m,3m.某廣告公司計劃在此空地上豎一塊長方形液晶廣告屏幕MNEF,MN:NE=16:9.線段MN必須過點P,端點M,N分別在邊AD,AB上,設(shè)AN=x(m),液晶廣告屏幕MNEF的面積為S(m2).
(1)用x的代數(shù)式表示AM,并寫出x的取值范圍;
(2)求S關(guān)于x的函數(shù)關(guān)系式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某市環(huán)保部門對市中心每天環(huán)境污染情況進(jìn)行調(diào)查研究,發(fā)現(xiàn)一天中環(huán)境污染指數(shù) 與時刻
與時刻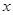 (時)的關(guān)系為
(時)的關(guān)系為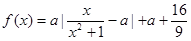 ,
, ,其中
,其中 是與氣象有關(guān)的參數(shù),且
是與氣象有關(guān)的參數(shù),且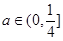 ,用每天
,用每天 的最大值作為當(dāng)天的污染指數(shù),記作
的最大值作為當(dāng)天的污染指數(shù),記作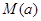 .
.
(1)令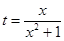 ,
, ,求
,求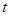 的取值范圍;
的取值范圍;
(2)按規(guī)定,每天的污染指數(shù)不得超過2,問目前市中心的污染指數(shù)是否超標(biāo)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某地需要修建一條大型輸油管道通過240公里寬的沙漠地帶,該段輸油管道兩端的輸油站已建好,余下工程是在該段兩端已建好的輸油站之間鋪設(shè)輸油管道和等距離修建增壓站(又稱泵站).經(jīng)預(yù)算,修建一個增壓站的工程費(fèi)用為400萬元,鋪設(shè)距離為 公里的相鄰兩增壓站之間的輸油管道費(fèi)用為
公里的相鄰兩增壓站之間的輸油管道費(fèi)用為 萬元.設(shè)余下工程的總費(fèi)用為
萬元.設(shè)余下工程的總費(fèi)用為 萬元.
萬元.
(1)試將 表示成
表示成 的函數(shù);
的函數(shù);
(2)需要修建多少個增壓站才能使 最小,其最小值為多少?
最小,其最小值為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) (x∈R,且x≠2).
(x∈R,且x≠2).
(1)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)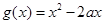 與函數(shù)
與函數(shù) 在x∈[0,1]上有相同的值域,求a的值.
在x∈[0,1]上有相同的值域,求a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如果n件產(chǎn)品中任取一件樣品是次品的概率為 ,則認(rèn)為這批產(chǎn)品中有
,則認(rèn)為這批產(chǎn)品中有 件次品。某企業(yè)的統(tǒng)計資料顯示,產(chǎn)品中發(fā)生次品的概率p與日產(chǎn)量n滿足
件次品。某企業(yè)的統(tǒng)計資料顯示,產(chǎn)品中發(fā)生次品的概率p與日產(chǎn)量n滿足
 ,有已知每生產(chǎn)一件正品可贏利a元,如果生產(chǎn)一件次品,非但不能贏利,還將損失
,有已知每生產(chǎn)一件正品可贏利a元,如果生產(chǎn)一件次品,非但不能贏利,還將損失 元(
元( ).
).
(1)求該企業(yè)日贏利額 的最大值;
的最大值;
(2)為保證每天的贏利額不少于日贏利額最大值的50%,試求該企業(yè)日產(chǎn)量的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
請你設(shè)計一個包裝盒,如圖所示, 是邊長為
是邊長為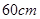 的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得
的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得 四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,
四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒, 在
在 上是被切去的等腰直角三角形斜邊的兩個端點,設(shè)
上是被切去的等腰直角三角形斜邊的兩個端點,設(shè) .
.
(1)若廣告商要求包裝盒側(cè)面積 最大,試問
最大,試問 應(yīng)取何值?
應(yīng)取何值?
(2)若廣告商要求包裝盒容積 最大,試問
最大,試問 應(yīng)取何值?并求出此時包裝盒的高與底面邊長的比值.
應(yīng)取何值?并求出此時包裝盒的高與底面邊長的比值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
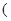 常數(shù)
常數(shù)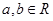 )滿足
)滿足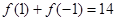 .
.
(1)求出 的值,并就常數(shù)
的值,并就常數(shù) 的不同取值討論函數(shù)
的不同取值討論函數(shù) 奇偶性;
奇偶性;
(2)若 在區(qū)間
在區(qū)間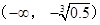 上單調(diào)遞減,求
上單調(diào)遞減,求 的最小值;
的最小值;
(3)在(2)的條件下,當(dāng) 取最小值時,證明:
取最小值時,證明: 恰有一個零點
恰有一個零點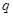 且存在遞增的正整數(shù)數(shù)列
且存在遞增的正整數(shù)數(shù)列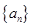 ,使得
,使得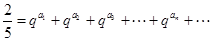 成立.
成立.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com