
如圖1,在等腰直角三角形 中,
中, ,
, ,
, 分別是
分別是 上的點,
上的點, ,
,
 為
為 的中點.將
的中點.將 沿
沿 折起,得到如圖2所示的四棱錐
折起,得到如圖2所示的四棱錐 ,其中
,其中 .
.

(Ⅰ) 證明: 平面
平面 ;
;
(Ⅱ) 求二面角 的平面角的余弦值.
的平面角的余弦值.
(Ⅰ)見解析 (Ⅱ) 
【解析】(Ⅰ) 在圖1中,易得
連結 ,在
,在 中,由余弦定理可得
中,由余弦定理可得

由翻折不變性可知 ,
,
所以 ,所以
,所以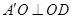 ,
,
理可證 , 又
, 又 ,所以
,所以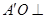 平面
平面 .
.

(Ⅱ) 傳統法:過 作
作 交
交 的延長線于
的延長線于 ,連結
,連結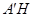 ,
,
因為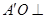 平面
平面 ,所以
,所以 ,
,
所以 為二面角
為二面角 的平面角.
的平面角.
結合圖1可知, 為
為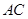 中點,故
中點,故 ,從而
,從而
所以 ,所以二面角
,所以二面角 的平面角的余弦值為
的平面角的余弦值為 .
.
向量法:以 點為原點,建立空間直角坐標系
點為原點,建立空間直角坐標系 如圖所示,
如圖所示,

則 ,
, ,
,
所以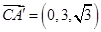 ,
,
設 為平面
為平面 的法向量,則
的法向量,則
 ,即
,即 ,解得
,解得 ,令
,令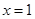 ,得
,得
由(Ⅰ) 知, 為平面
為平面 的一個法向量,
的一個法向量,
所以 ,即二面角
,即二面角 的平面角的余弦值為
的平面角的余弦值為 .
.
解決折疊問題,需注意一下兩點:1.一定要關注“變量”和“不變量”在證明和計算中的應用:折疊時位于棱同側的位置關系和數量關系不變;位于棱兩側的位置關系與數量關系變;2.折前折后的圖形結合起來使用.如本題第一問,關鍵是由翻折不變性可知 ,借助勾股定理進行證明垂直關系;(2)利用三垂線定理法或者空間向量法求解二面角. 求二面角:關鍵是作出或找出其平面角,常用做法是利用三垂線定理定角法,先找到一個半平面的垂線,然后過垂足作二面角棱的垂線,再連接第三邊,即可得到平面角。若考慮用向量來求:要求出二個面的法向量,然后轉化為
,借助勾股定理進行證明垂直關系;(2)利用三垂線定理法或者空間向量法求解二面角. 求二面角:關鍵是作出或找出其平面角,常用做法是利用三垂線定理定角法,先找到一個半平面的垂線,然后過垂足作二面角棱的垂線,再連接第三邊,即可得到平面角。若考慮用向量來求:要求出二個面的法向量,然后轉化為 ,要注意兩個法向量的夾角與二面角可能相等也可能互補,要從圖上判斷一下二面角是銳二面角還是鈍二面角,然后根據余弦值確定相等或互補即可。
,要注意兩個法向量的夾角與二面角可能相等也可能互補,要從圖上判斷一下二面角是銳二面角還是鈍二面角,然后根據余弦值確定相等或互補即可。
【考點定位】考查折疊問題和二面角的求解,考查空間想象能力和計算能力.


科目:高中數學 來源: 題型:
 如圖,在平面直角坐標系xoy中,拋物線y=
如圖,在平面直角坐標系xoy中,拋物線y=| 1 |
| 18 |
| 4 |
| 9 |
| 9 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,一個等腰直角三角形的硬紙片△ABC中,∠ACB=90°,AC=4cm,CD是斜邊上的高,沿CD把△ABC折成直二面角.
如圖,一個等腰直角三角形的硬紙片△ABC中,∠ACB=90°,AC=4cm,CD是斜邊上的高,沿CD把△ABC折成直二面角.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•廣州二模)如圖,一個等腰直角三角形的直角邊長為2,分別以三個頂點為 圓心,l為半徑在三角形內作圓弧,三段圓弧與斜邊圍成區域M (圖中白色部分).若在此三角形內隨機取一點P,則點P落在區 域M內的概率為
(2013•廣州二模)如圖,一個等腰直角三角形的直角邊長為2,分別以三個頂點為 圓心,l為半徑在三角形內作圓弧,三段圓弧與斜邊圍成區域M (圖中白色部分).若在此三角形內隨機取一點P,則點P落在區 域M內的概率為| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省廣州市畢業班綜合測試(二)文科數學試卷(解析版) 題型:填空題
如圖,一個等腰直角三角形的直角邊長為2,分別以三個頂點為圓心,1為半徑在三角形內作圓弧,三段圓弧與斜邊圍成區域 (圖中白色部分).若在此三角形內隨機取一點
(圖中白色部分).若在此三角形內隨機取一點 ,則點
,則點 落在區域
落在區域 內的概率為 .
內的概率為 .

查看答案和解析>>
科目:高中數學 來源: 題型:
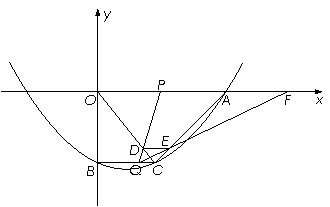
如圖,在平面直角坐標系xoy中,拋物線y=![]() x 2-
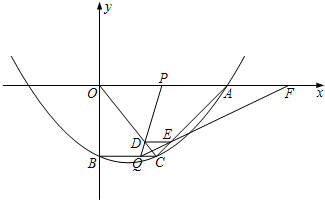
x 2-![]() x-10與x軸的交點為A,與y軸的交點為點B,過點B作x軸的平行線BC,交拋物線于點C,連結AC.現有兩動點P,Q分別從O,C兩點同時出發,點P以每秒4個單位的速度沿OA向終點A移動,點Q以每秒1個單位的速度沿CB向點B移動,點P停止運動時,點Q也同時停止運動.線段OC,PQ相交于點D,過點D作DE∥OA,交CA于點E,射線QE交x軸于點F.設動點P,Q移動的時間為t(單位:秒)
x-10與x軸的交點為A,與y軸的交點為點B,過點B作x軸的平行線BC,交拋物線于點C,連結AC.現有兩動點P,Q分別從O,C兩點同時出發,點P以每秒4個單位的速度沿OA向終點A移動,點Q以每秒1個單位的速度沿CB向點B移動,點P停止運動時,點Q也同時停止運動.線段OC,PQ相交于點D,過點D作DE∥OA,交CA于點E,射線QE交x軸于點F.設動點P,Q移動的時間為t(單位:秒)
(1)求A,B,C三點的坐標和拋物線的頂點坐標;
(2)當t為何值時,四邊形PQCA為平行四邊形?請寫出計算過程;
(3)當t∈(0,![]() )時,△PQF的面積是否總為定值?若是,求出此定值;若不是,請說明理由;
)時,△PQF的面積是否總為定值?若是,求出此定值;若不是,請說明理由;
(4)當t為何值時,△PQF為等腰三角形?請寫出解答過程.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com